题目内容
在锐角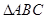 中,角
中,角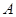 ,
,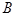 ,
,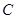 对应的边分别是
对应的边分别是 ,
,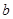 ,
,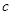 .已知
.已知 .
.
(1)求角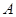 的大小;
的大小;
(2)若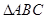 的面积
的面积 ,
,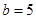 ,求
,求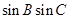 的值.
的值.
(1)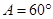 ;(2)
;(2)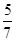 .
.
解析试题分析:(1)把已知的等式变形为: 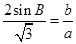 ,并利用正弦定理化简,根据
,并利用正弦定理化简,根据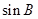 不为0,可得出
不为0,可得出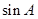 的值,由三角形为锐角三角形,得出
的值,由三角形为锐角三角形,得出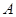 为锐角,利用特殊角的三角函数值即可求出
为锐角,利用特殊角的三角函数值即可求出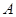 的度数;(2)由面积公式
的度数;(2)由面积公式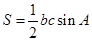 求得
求得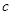 ,由余弦定理
,由余弦定理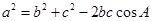 计算出
计算出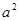 ,由
,由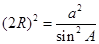 计算出
计算出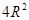 ,最后由正弦定理化简
,最后由正弦定理化简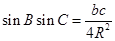 ,代入数值即可得到结果.
,代入数值即可得到结果.
试题解析:(1)由 可得
可得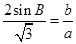 ,而
,而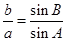 ,所以
,所以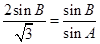
因为 为三角形的内角,所以
为三角形的内角,所以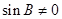 ,所以由
,所以由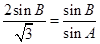 可得
可得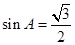
又因为 为锐角三角形,所以
为锐角三角形,所以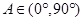 ,所以
,所以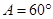 6分
6分
(2)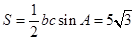
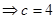 ,由余弦定理得:
,由余弦定理得: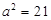
由正弦定理可知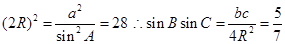
或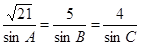
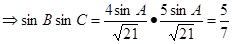 12分.
12分.
考点:正余弦定理在解三角形中的应用,面积公式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 c+bcosC.
c+bcosC. ,求b的最小值.
,求b的最小值. 中,角
中,角 的对边分别为
的对边分别为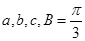 ,
,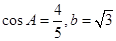 。
。 的值;
的值;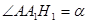 .
.
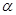 表示
表示 的面积;
的面积; ,b=
,b= ,求c;
,求c; 的取值范围.
的取值范围.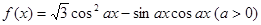 的图像与直线
的图像与直线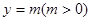 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为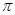 的等差数列.
的等差数列.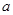 和
和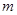 的值;
的值;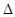 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若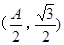 是函数
是函数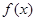 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求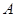 为
为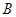 ,
, 的等差中项.
的等差中项.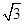 ,求b,c的值.
,求b,c的值. 中,角
中,角 ,
, ,
,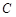 所对的边分别是
所对的边分别是 ,
,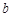 ,
,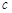 ,已知
,已知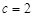 ,
,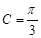 .
.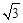 ,求
,求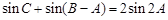 ,求
,求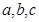 分别为角A、B、C的对边,
分别为角A、B、C的对边,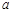 =3,△ABC的面积为6,
=3,△ABC的面积为6, ,D为△ABC内任一点,点D到三边距离之和为
,D为△ABC内任一点,点D到三边距离之和为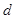 。
。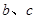 ;
;