题目内容
20.若f′(1)=2012,则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=2012,$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{-△x}$=-2012,$\underset{lim}{△x→0}$$\frac{f(1)-f(1+△x)}{4△x}$=-503,$\underset{lim}{△x→0}$$\frac{f(1+2△x)-f(1)}{△x}$=4024.分析 根据导数的定义分别进行计算即可.
解答 解:$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=f′(1)=2012,
$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{-△x}$=-$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=-f′(1)=-2012,
$\underset{lim}{△x→0}$$\frac{f(1)-f(1+△x)}{4△x}$=$-\frac{1}{4}$•$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=$-\frac{1}{4}$•f′(1)=$-\frac{1}{4}$×2012=-503,
$\underset{lim}{△x→0}$$\frac{f(1+2△x)-f(1)}{△x}$=2×$\underset{lim}{△x→0}\frac{f(1+2△x)-f(1)}{2△x}$=2f′(1)=2×2012=4024.
故答案为:2012;-2012;-503;4024
点评 本题主要考查导数的计算,根据导数的极限定义是解决本题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
8.定义在R上的偶函数y=f(x)满足f(x+1)=-f(x),且当x∈(0,1]时单调递增,则( )
| A. | $f(\frac{1}{3})<f(-5)<f(\frac{5}{2})$ | B. | $f(\frac{1}{3})<f(\frac{5}{2})<f(-5)$ | C. | $f(\frac{5}{2})<f(\frac{1}{3})<f(-5)$ | D. | $f(-5)<f(\frac{1}{3})<f(\frac{5}{2})$ |
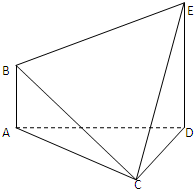 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1.
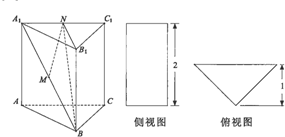
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1. 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,直线A1B与平面BB1C1C所成角的大小为arctan$\frac{{\sqrt{5}}}{5}$.求三棱锥C1-A1BC的体积.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,直线A1B与平面BB1C1C所成角的大小为arctan$\frac{{\sqrt{5}}}{5}$.求三棱锥C1-A1BC的体积.