题目内容
15.已知三棱柱ABC=A1B1C1的侧棱BB1⊥底面ABC,其侧视图与俯视图如图所示,AB=BC且AB⊥BC,M,N分别是A1B,A1C1的中点.(1)求证:MN∥平面BCC1B1;
(2)求三棱锥B-A1B1N的体积.
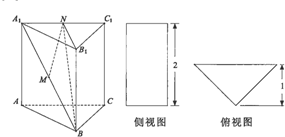
分析 (1)连接BC1,利用三角形的中位线定理可得:MN∥BC1,再利用线面平行的判定定理可得:MN∥平面BCC1B1;
(2)由侧视图与俯视图可知:BB1=2,B1N=1,再利用等腰直角三角形的性质可得:A1C1=2=2A1N.B1N⊥A1C1.利用三棱锥B-A1B1N的体积V=$\frac{1}{3}{S}_{△{A}_{1}{B}_{1}N}$×BB1即可得出.
解答 (1)证明:连接BC1,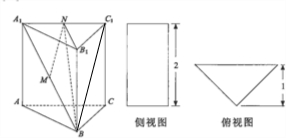
∵M,N分别是A1B,A1C1的中点.
∴MN∥BC1,
又MN?平面BCC1B1,BC1?平面BCC1B1;
∴MN∥平面BCC1B1;
(2)解:由侧视图与俯视图可知:BB1=2,B1N=1,
∵A1B1=B1C1且A1B1⊥B1C1,N是A1C1的中点,
∴A1C1=2=2A1N.B1N⊥A1C1.
∴三棱锥B-A1B1N的体积V=$\frac{1}{3}{S}_{△{A}_{1}{B}_{1}N}$×BB1=$\frac{1}{3}×\frac{1}{2}×1×1$×2=$\frac{1}{3}$.
点评 本题考查了三角形的中位线定理、线面平行与垂直的判定性质定理、三视图的性质、等腰直角三角形的性质、三棱锥体积计算公式、三棱柱的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10.若函数f(x)=$\frac{sinx}{x}$,并且$\frac{π}{3}$<a<b<$\frac{2π}{3}$,则下列各结论中正确的是( )
| A. | f(a)<f($\sqrt{ab}$)<f($\frac{a+b}{2}$) | B. | f($\sqrt{ab}$)<f($\frac{a+b}{2}$)<f(b) | C. | f($\sqrt{ab}$)<f($\frac{a+b}{2}$)<f(a) | D. | f(b)<f($\frac{a+b}{2}$)<f($\sqrt{ab}$) |
7.将函数y=sin$\frac{x}{2}$的图象按向量$\overrightarrow{a}$平移后,得到y=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象,则向量$\overrightarrow{a}$的坐标可能为( )
| A. | ($\frac{π}{2}$,0) | B. | (-$\frac{π}{2}$,0) | C. | ($\frac{π}{4}$,0) | D. | (-$\frac{π}{4}$,0) |