Question

【题目】在极坐标系中，曲线C1：ρ=2cosθ，曲线C2：ρ=（ρcosθ+4）cosθ．以极点为坐标原点，极轴为x轴正半轴建立直角坐标系xOy，曲线C的参数方程为 （t为参数）． （Ⅰ）求C1 ， C2的直角坐标方程；
（Ⅱ）C与C1 ， C2交于不同四点，这四点在C上的排列顺次为H，I，J，K，求||HI|﹣|JK||的值．

Answer 1

【答案】解：（Ⅰ）∵曲线C1：ρ=2cosθ，∴ρ2=2ρcosθ， ∵ρ2=x2+y2 ， x=ρcosθ，y=ρsinθ，
∴曲线C1的直角坐标方程为（x﹣1）2+y2=1．
∵曲线C2：ρ=（ρcosθ+4）cosθ．
∴ρ2sin2θ=4ρcosθ，
∴曲线C2的直角坐标方程为y2=4x．
（Ⅱ）不妨设四点在C上的排列顺次至上而下为H，I，J，K，
它们对应的参数分别为t1 ， t2 ， t3 ， t4 ， 如图，连结C1 ， J，
则△C1IJ为正三角形，
∴|IJ|=1，||HI|﹣|JK||=||HI|﹣|IK|+|IJ||=||t1|﹣|t4|+1|=|﹣（t1+t4）+1|，
把曲线C的参数方程为 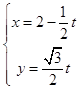（t为参数）代入y2=4x，
得： ，即3t2+8t﹣32=0，故 ，
∴||HI|﹣|JK||= ．

【解析】（Ⅰ）由ρ2=x2+y2 ， x=ρcosθ，y=ρsinθ，能求出C1 ， C2的直角坐标方程．（Ⅱ）设四点在C上的排列顺次至上而下为H，I，J，K，它们对应的参数分别为t1 ， t2 ， t3 ， t4 ， 连结C1 ， J，则△C1IJ为正三角形，||HI|﹣|JK||=||HI|﹣|IK|+|IJ||=||t1|﹣|t4|+1|=|﹣（t1+t4）+1|，把曲线C的参数方程代入y2=4x，得3t2+8t﹣32=0，由此能求出||HI|﹣|JK||的值．