题目内容
已知函数f(x)=lg[(a2-1)x2+(a+1)x+1],设命题p:“f(x)的定义域为R”;命题q:“f(x)的值域为R”。
(1)若命题p为真,求实数a的取值范围;
(2)若命题q为真,求实数a的取值范围;
(3)问: p是q的什么条件?请说明理由。
p是q的什么条件?请说明理由。
(1)若命题p为真,求实数a的取值范围;
(2)若命题q为真,求实数a的取值范围;
(3)问:
 p是q的什么条件?请说明理由。
p是q的什么条件?请说明理由。解:(1)命题p为真,即f(x)的定义域为R,
等价于(a2-1)x2+(a+1)x+1>0恒成立,
等价于a=-1或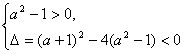 解得a≤-1或
解得a≤-1或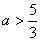
∴实数a的取值范围为(-∞,-1]∪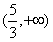 。
。
(2)命题q为真,即f(x)的值域是R,
等价于u=(a2-1)x2+(a+1)x+1的值域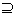 (0,+∞),
(0,+∞),
等价于a=1或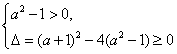
解得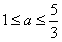
∴实数a的取值范围为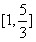 。
。
(3)由(1)(2)知,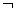 p:
p: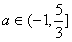
q: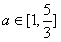
而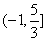
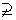
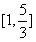
∴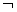 p是q的必要而不充分的条件。
p是q的必要而不充分的条件。
等价于(a2-1)x2+(a+1)x+1>0恒成立,
等价于a=-1或
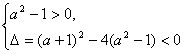 解得a≤-1或
解得a≤-1或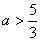
∴实数a的取值范围为(-∞,-1]∪
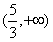 。
。(2)命题q为真,即f(x)的值域是R,
等价于u=(a2-1)x2+(a+1)x+1的值域
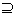 (0,+∞),
(0,+∞),等价于a=1或
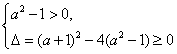
解得
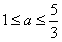
∴实数a的取值范围为
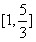 。
。(3)由(1)(2)知,
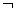 p:
p: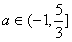
q:
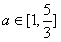
而
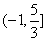
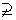
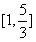
∴
 p是q的必要而不充分的条件。
p是q的必要而不充分的条件。
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目