题目内容
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:(1)试判断A1是否在平面B1CD内;(回答是与否)
(2)求异面直线B1D1与C1D所成的角;
(3)如果用图示中这样一个装置来盛水,那么最多可以盛多少体积的水.
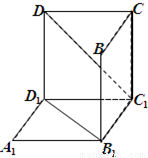
【答案】分析:(1)利用正方体对角面是平行四边形的性质即可得出;
(2)利用对角面的性质、表面对角线组成的△AB1D1是等边三角形即可求出;
(3)题目中的图形一个装置来盛水,那么盛最多体积的水时应是三棱锥C1-B1CD1的体积.
解答:解:(1)是.补全正方体如图所示:
证明如下:连接A1D、B1C,∵A1B1∥DC,A1B1=DC,
∴四边形A1B1CD是平行四边形,
∴A1是在平面B1CD内;
(2)连接AB1、AD1,∵对角面AB1C1D是矩形,∴AB1∥DC1,
∴∠AB1D1或其补角是异面直线B1D1与C1D所成的角.
∵AD1=AB1=D1B1,∴△AB1D1是正三角形.
∴∠AB1D1=60°.
∴异面直线B1D1与C1D所成的角是60°.
(3)题目中的图形一个装置来盛水,那么盛最多体积的水时应是
三棱锥C1-B1CD1的体积.
又 .
.
∴用图示中这样一个装置来盛水,那么最多可以盛 体积的水.
体积的水.
点评:熟练掌握正方体对角面、表面对角线的性质及三棱锥的体积计算公式是解题的关键.
(2)利用对角面的性质、表面对角线组成的△AB1D1是等边三角形即可求出;
(3)题目中的图形一个装置来盛水,那么盛最多体积的水时应是三棱锥C1-B1CD1的体积.
解答:解:(1)是.补全正方体如图所示:

证明如下:连接A1D、B1C,∵A1B1∥DC,A1B1=DC,
∴四边形A1B1CD是平行四边形,
∴A1是在平面B1CD内;
(2)连接AB1、AD1,∵对角面AB1C1D是矩形,∴AB1∥DC1,
∴∠AB1D1或其补角是异面直线B1D1与C1D所成的角.
∵AD1=AB1=D1B1,∴△AB1D1是正三角形.
∴∠AB1D1=60°.
∴异面直线B1D1与C1D所成的角是60°.
(3)题目中的图形一个装置来盛水,那么盛最多体积的水时应是
三棱锥C1-B1CD1的体积.
又
 .
.∴用图示中这样一个装置来盛水,那么最多可以盛
 体积的水.
体积的水.点评:熟练掌握正方体对角面、表面对角线的性质及三棱锥的体积计算公式是解题的关键.

练习册系列答案
相关题目
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: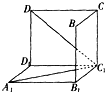 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的几何图形.
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的几何图形.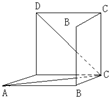 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的. 的正方体
的正方体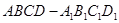 中分离出来的:
中分离出来的: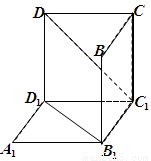
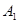 是否在平面
是否在平面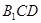 内;(回答是与否)
内;(回答是与否)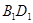 与
与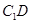 所成的角;
所成的角;