题目内容
设命题:p:向量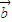 与
与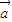 共线,命题q:有且只有一个实数λ,使得
共线,命题q:有且只有一个实数λ,使得 =
=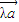 ,则p是q的( )
,则p是q的( )A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
【答案】分析:先分析p⇒q是否为真命题,再分析q⇒p是否为真命题.
解答:解:若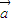 =
=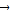 ,
,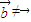 则,任意实数λ,都有
则,任意实数λ,都有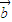 =
=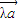 不成立
不成立
即:p⇒q为假命题
若有且只有一个实数λ,使得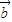 =
=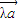
则向量 与
与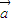 共线
共线
即q⇒p为真命题.
综上:p是q的必要不充分条件
故选B
点评:本题考查的关键是向量平行(共线)的充要条件:向量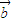 与
与 共线,有且只有一个实数λ,使得
共线,有且只有一个实数λ,使得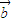 =
=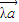 (
(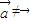 )
)
解答:解:若
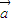 =
=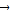 ,
,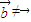 则,任意实数λ,都有
则,任意实数λ,都有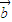 =
=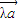 不成立
不成立即:p⇒q为假命题
若有且只有一个实数λ,使得
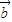 =
=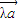
则向量
 与
与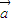 共线
共线即q⇒p为真命题.
综上:p是q的必要不充分条件
故选B
点评:本题考查的关键是向量平行(共线)的充要条件:向量
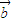 与
与 共线,有且只有一个实数λ,使得
共线,有且只有一个实数λ,使得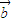 =
=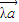 (
(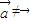 )
) 
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
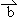 与
与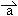 共线,命题Q:有且只有一个实数
共线,命题Q:有且只有一个实数 ,使得
,使得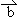 与
与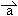 共线,命题Q:有且只有一个实数
共线,命题Q:有且只有一个实数 ,使得
,使得 与
与 共线,命题q:有且只有一个实数λ,使得
共线,命题q:有且只有一个实数λ,使得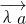 ,则p是q的
,则p是q的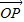 =
=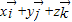 (其中
(其中 分别为x轴、y轴、z轴正方向上的单位向量).有下列命题:
分别为x轴、y轴、z轴正方向上的单位向量).有下列命题: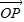 =
=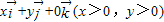 且|
且|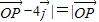
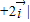 ,则
,则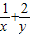 的最小值为2
的最小值为2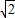

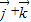 ,若向量
,若向量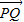 与
与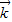 共线且|
共线且|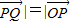 |,则动点P的轨迹是抛物线;
|,则动点P的轨迹是抛物线;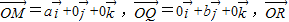 =
=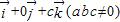 ,则平面MQR内的任意一点A(x,y,z)的坐标必须满足关系式
,则平面MQR内的任意一点A(x,y,z)的坐标必须满足关系式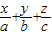 =1;
=1;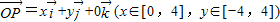 ,
,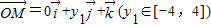 ,
,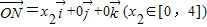 ,若向量
,若向量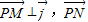 与
与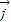 共线且|
共线且|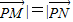 |,则动点P的轨迹是双曲线的一部分.
|,则动点P的轨迹是双曲线的一部分.