题目内容
(本小题满分15分)、已知: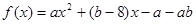 ,当
,当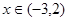 时,
时,
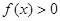 ;
;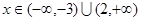 时,
时,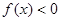
(1)求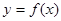 的解析式
的解析式
(2)c为何值时,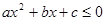 的解集为R.
的解集为R.
【答案】
⑴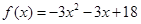 ;⑵当
;⑵当 时
时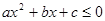 的解集为R.
的解集为R.
【解析】
试题分析:(1)根据f(x)>0和f(x)<0的解集可知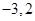 是是方程
是是方程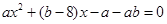 的两根,然后借助韦达定理建立关于a,b的方程,求出a,b的值.
的两根,然后借助韦达定理建立关于a,b的方程,求出a,b的值.
(2)在(1)的基础上,可知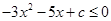 的解集为R,因为
的解集为R,因为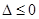 ,从而得到关于c的不等式,解出c的范围.
,从而得到关于c的不等式,解出c的范围.
所以
⑴由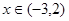 时,
时,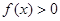 ;
;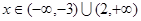 时,
时,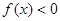
知: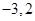 是是方程
是是方程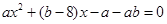 的两根
的两根
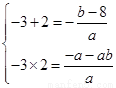
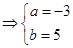
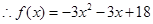
⑵由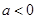 ,知二次函数
,知二次函数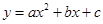 的图象开口向下
的图象开口向下
要使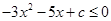 的解集为R,只需
的解集为R,只需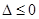
即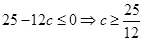
∴当 时
时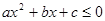 的解集为R.
的解集为R.
考点:一元二次不等式与一元二次方程,一元二次函数图像之间的对应关系,一元二次不等式恒成立问题.
点评:解一元二次不等式要先求出对应的一元二次方程的根,然后要注意对应的二次函数的开口方向,然后再根据不等式的符号,来考虑解集情况,涉及到一元二次不等式恒成立问题除考虑开口方向之外,还要借助判别式求解.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.