题目内容
2003 年10 月15 日9 时，“神舟五号”载人飞船发射升空，于9 时9 分50 秒准确进入预定轨道，开始巡天飞行．该轨道是以地球的中心F2 为一个焦点的椭圆．选取坐标系如图所示，椭圆中心在原点，近地点A 距地面200 km ，远地点B 距地面350 km ．已知地球半径R= 6 371 km.
（1）求飞船飞行的椭圆轨道的方程；
（2）飞船绕地球飞行了十四圈后，于16日5时59分返回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约6×105km，问飞船巡天飞行平均速度是多少？（结果精确到1 km/s ）
（1）求飞船飞行的椭圆轨道的方程；
（2）飞船绕地球飞行了十四圈后，于16日5时59分返回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约6×105km，问飞船巡天飞行平均速度是多少？（结果精确到1 km/s ）
解：（1）设椭圆的方程为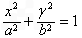
由题设条件得a-c=|OA|-|OF2|=|F2A|=6371+200=6571,
a+c=|OB|+|OF2|=|F2B|=6371+350=6721,
解得a=6646，c=75.
所以a2=44169316，b2=a2-c2=(a+c)(a-c)=44163 691.
所以椭圆的方程为
（2）从15日9时到16日6时共21个小时，合21×3600秒，减去开始的9分50秒，即9×60+50=590（s），再减去最后多计的1分钟，共计590+60=650（s），飞船巡天飞行时间是21×3 600-650=74950（s），平均速度是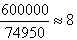
（km/s）.
所以飞船巡天飞行的平均速度是8 km/s．
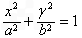
由题设条件得a-c=|OA|-|OF2|=|F2A|=6371+200=6571,
a+c=|OB|+|OF2|=|F2B|=6371+350=6721,
解得a=6646，c=75.
所以a2=44169316，b2=a2-c2=(a+c)(a-c)=44163 691.
所以椭圆的方程为
（2）从15日9时到16日6时共21个小时，合21×3600秒，减去开始的9分50秒，即9×60+50=590（s），再减去最后多计的1分钟，共计590+60=650（s），飞船巡天飞行时间是21×3 600-650=74950（s），平均速度是
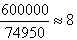（km/s）.所以飞船巡天飞行的平均速度是8 km/s．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
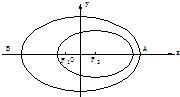2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行．该轨道是以地球的中心F2为一个焦点的椭圆．选取坐标系如图所示，椭圆中心在原点．近地点A距地面200km，远地点B距地面350km．已知地球半径R=6371km．
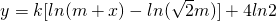（其中k≠0，lnx是以e为底x的对数）．当燃料重量为
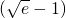m吨时，该火箭的最大速度为4（km/s）．
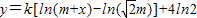（其中k≠0，lnx是以e为底x的对数）．当燃料重量为
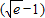m吨时，该火箭的最大速度为4（km/s）．