题目内容
若复数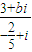 的实部和虚部互为相反数,且在(ax+1)b(a≠0)展开式中,x3项的系数是x2项系数与x5项系数的等比中项,则a=( )
的实部和虚部互为相反数,且在(ax+1)b(a≠0)展开式中,x3项的系数是x2项系数与x5项系数的等比中项,则a=( )A.
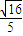
B.
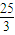
C.

D.
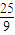
【答案】分析:利用复数的除法运算法则求出复数的实部、虚部,列出方程解出b;代入二项式,利用二项展开式的通项公式求出通项,求出三项的系数,列出方程求出a.
解答:解: =
=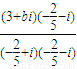 =
=
∵实部和虚部互为相反数
∴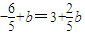 解得b=7
解得b=7
(ax+1)b展开式的通项为Tr+1=Cbr(ax)r=arC7rxr
x3,x2,x5的系数分别是a3C73,a2C72,a5C75
∴(a3C73)2=a2C72•a5C75解得a=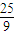
故选D.
点评:本题考查复数的除法运算法则;利用二项展开式的通项公式求特定项问题.
解答:解:
 =
=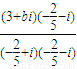 =
=
∵实部和虚部互为相反数
∴
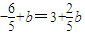 解得b=7
解得b=7(ax+1)b展开式的通项为Tr+1=Cbr(ax)r=arC7rxr
x3,x2,x5的系数分别是a3C73,a2C72,a5C75
∴(a3C73)2=a2C72•a5C75解得a=
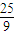
故选D.
点评:本题考查复数的除法运算法则;利用二项展开式的通项公式求特定项问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于复数z=
,下列说法中正确的是( )
| (1+i)2 |
| 1-i |
| A、在复平面内复数z对应的点在第一象限 | ||
B、复数z的共轭复数
| ||
| C、若复数z1=z+b(b∈R)为纯虚数,则b=1 | ||
| D、设a,b为复数z的实部和虚部,则点(a,b)在以原点为圆心,半径为1的圆上 |