题目内容
 (I)A为△ABC的内角,则sinA+cosA的取值范围是________.
(I)A为△ABC的内角,则sinA+cosA的取值范围是________.
(II)给定两个长度为1的平面向量 和
和 ,它们的夹角为120°.
,它们的夹角为120°.
如图所示,点C在以O为圆心的圆弧 上变动.若
上变动.若 ,其中x,y∈R,则x+y的最大值是________.
,其中x,y∈R,则x+y的最大值是________.
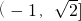 2
2分析:(I)根据辅助角公式,我们可以将sinA+cosA化为正弦型函数的形式,根据A为△ABC的内角,即可得到sinA+cosA的取值范围;
(II)∠AOC=α,我们可以得到x,y的解析式(含参数α),根据辅助角公式,我们可以得到x+y的表达式,然后根据三角函数的性质,即可得到x+y的最大值.
解答:(I)∵sinA+cosA=
 sin(A+
sin(A+ )
)又∵A∈(0,π)
∴
 sin(A+
sin(A+ )∈
)∈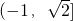 ;
;(II)设∠AOC=α
∴
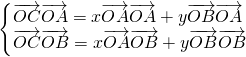
即
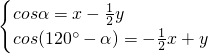
∴x+y=2[cosα+cos(120°-α)]=cosα+
 sinα=2sin(x+
sinα=2sin(x+ )≤2
)≤2故x+y的最大值是 2
故答案为:
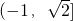 ,2
,2点评:本题考查的知识点是正弦函数的值域,向量的加法及其几何意义,熟练掌握辅助角公式及正弦型函数的性质是解答本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 (I)A为△ABC的内角,则sinA+cosA的取值范围是
(I)A为△ABC的内角,则sinA+cosA的取值范围是

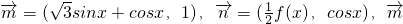 ∥
∥ .
.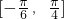 内的值域;
内的值域;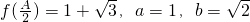 ,求△ABC的面积.
,求△ABC的面积.