题目内容
 如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则
如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则
- A.e1<e2
- B.e1>e2
- C.e1=e2
- D.e1和e2大小关系不确定
B
分析:先根据题意和图形可得到a1=2a2,c1>2c2,进而根据不等式的性质可得到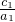 >
>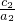 ,即可得到答案.
,即可得到答案.
解答:由题意知,a1=2a2,c1>2c2,
∴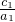 >
>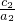 ,即e1>e2.
,即e1>e2.
∴正确的为B.
故选B.
点评:本题主要考查椭圆的基本性质的应用.圆锥曲线是高考的重点内容,椭圆的基本性质更是高考的重点,更要准备充分.
分析:先根据题意和图形可得到a1=2a2,c1>2c2,进而根据不等式的性质可得到
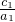 >
>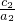 ,即可得到答案.
,即可得到答案.解答:由题意知,a1=2a2,c1>2c2,
∴
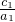 >
>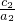 ,即e1>e2.
,即e1>e2.∴正确的为B.
故选B.
点评:本题主要考查椭圆的基本性质的应用.圆锥曲线是高考的重点内容,椭圆的基本性质更是高考的重点,更要准备充分.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图,椭圆
如图,椭圆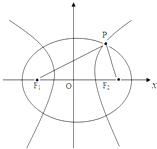 如图:椭圆
如图:椭圆 (2013•崇明县一模)如图,椭圆
(2013•崇明县一模)如图,椭圆 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C: