Question

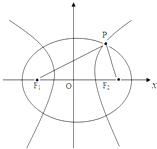如图：椭圆

x2

49

+

y2

b2

=1（0＜b＜7）与双曲线x²-

y2

n2

=1有相同的焦点F₁，F₂，且∠F₁PF₂=90°，P是两曲线的一个公共点，则|F₁F₂|的值为（　　）

A．6

B．8

C．10

D．12

Answer 1

分析：由椭圆和双曲线的定义得到P点到两个焦点距离的和与差，联立方程组分别求出两个距离，然后直接由勾股定理求得答案．

解答：解：设F₁（-c，0），F₂（c，0）．
由椭圆

x2

49

+

y2

b2

=1（0＜b＜7），知其半长轴长为7．
由双曲线x²-

y2

n2

=1，知，其实半轴长为1．
不妨设P为两曲线在第一象限内的公共点，
则|PF₁|+|PF₂|=14，|PF₁|-|PF₂|=2．
解得|PF₁|=8，|PF₂|=6．
因为∠F₁PF₂=90°，所以|F1F2|2=|PF1|2+|PF2|2=8²+6²=100．
所以|F₁F₂|=10．
故选C．

点评：本题是圆锥曲线的综合题，考查了椭圆和双曲线的定义，训练了勾股定理，是中档题．