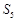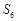题目内容
(本小题满分12分)
已知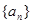 是公差不为零的等差数列,
是公差不为零的等差数列, 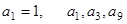 成等比数列.
成等比数列.
(1)求数列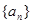 的通项; (2)求数列
的通项; (2)求数列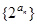 的前n项和
的前n项和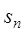
已知
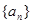 是公差不为零的等差数列,
是公差不为零的等差数列, 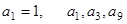 成等比数列.
成等比数列.(1)求数列
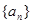 的通项; (2)求数列
的通项; (2)求数列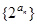 的前n项和
的前n项和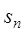
(1)an=n. (2) Sm=2+22+23+…+2n=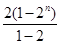 =2n+1-2.
=2n+1-2.
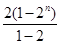 =2n+1-2.
=2n+1-2. 本试题主要是考查了数列的通项公式的求解,以及数列的求和综合运用。
(1)由题设知公差d≠0,由a1=1,a1,a3,a9成等比数列得,得到d=1,可得通项公式。
(2)由上一问可知,数列的通项公式是等比数列,那么根据公式得到结论。
解 (1)由题设知公差d≠0,
由a1=1,a1,a3,a9成等比数列得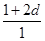 =
=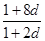 ,
,
解得d=1,d=0(舍去), 故{an}的通项an=1+(n-1)×1=n.………6分
(2)由(Ⅰ)知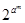 =2n,由等比数列前n项和公式得
=2n,由等比数列前n项和公式得
Sm=2+22+23+…+2n=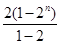 =2n+1-2. ………12分
=2n+1-2. ………12分
(1)由题设知公差d≠0,由a1=1,a1,a3,a9成等比数列得,得到d=1,可得通项公式。
(2)由上一问可知,数列的通项公式是等比数列,那么根据公式得到结论。
解 (1)由题设知公差d≠0,
由a1=1,a1,a3,a9成等比数列得
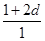 =
=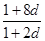 ,
,解得d=1,d=0(舍去), 故{an}的通项an=1+(n-1)×1=n.………6分
(2)由(Ⅰ)知
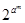 =2n,由等比数列前n项和公式得
=2n,由等比数列前n项和公式得Sm=2+22+23+…+2n=
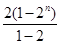 =2n+1-2. ………12分
=2n+1-2. ………12分
练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
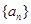 满足
满足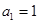 ,
,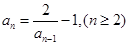 ,则
,则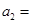 ( )
( )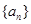 是公比大于1的等比数列,
是公比大于1的等比数列,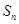 为数列
为数列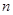 项和。
项和。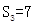 ,且
,且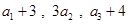 构成等差数列.
构成等差数列.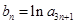 ,求数列
,求数列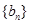 的前
的前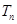 .
.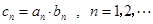 ,求数列
,求数列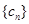 的前
的前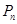 .
.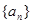
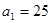 ,
,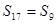
 哪一个最大?并求出最大值
哪一个最大?并求出最大值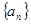 的首项
的首项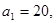 前
前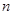 项和记为
项和记为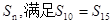 ,求
,求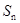 取得最大值,并求出最大值.
取得最大值,并求出最大值. 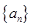 的前
的前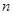 项和为
项和为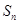 ,若
,若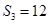 ,且
,且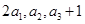 成等比数列.
成等比数列.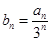 的前
的前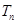 ,求证
,求证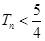 .
.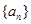 中,若
中,若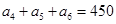 ,则
,则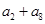 的值为 .
的值为 .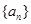 中,
中, 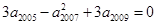 ,数列
,数列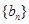 是等比数列,且
是等比数列,且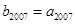 ,则
,则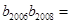 ( )
( )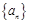 是等差数列,
是等差数列,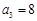 ,
,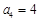 ,则前
,则前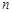 项和
项和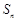 中最大的是( )
中最大的是( )
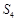 或
或