题目内容

（2013•黄埔区一模）若z=cosθ+isinθ（θ∈R，i是虚数单位），则|z-2-2i|的最小值是（　　）
分析：易得复数z表示的点在单位圆上，而要求的值为单位圆上的点到复数2+2i表示的点Z的距离，由数形结合的思想可得答案．
解答：解：由复数的几何意义可知：z=cosθ+isinθ表示的点在单位圆上，
而|z-2-2i|表示该单位圆上的点到复数2+2i表示的点Z的距离，

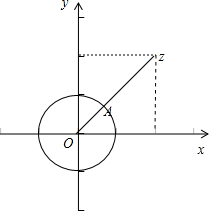
由图象可知：|z-2-2i|的最小值应为点A到Z的距离，
而OZ=
22+22
=2
2
，圆的半径为1，
故|z-2-2i|的最小值为2
2
-1，
故选D
点评：本题考查复数的模长的最值，涉及复数的几何意义和数形结合的思想，属基础题．
练习册系列答案
相关题目
（2013•黄埔区一模）给定椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，称圆心在原点O、半径是
a2+b2
的圆为椭圆C的“准圆”．已知椭圆C的一个焦点为F(
2
，0)，其短轴的一个端点到点F的距离为
3
．
（1）求椭圆C和其“准圆”的方程；
（2）若点A是椭圆C的“准圆”与x轴正半轴的交点，B，D是椭圆C上的两相异点，且BD⊥x轴，求
AB
•
AD
的取值范围；
（3）在椭圆C的“准圆”上任取一点P，过点P作直线l1，l2，使得l1，l2与椭圆C都只有一个交点，试判断l1，l2是否垂直？并说明理由．
（2013•黄埔区一模）对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R+，且f（1）=3．
（1）若（1，1）是f（x）的一个“P数对”，求f（2n）（n∈N*）；
（2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2n）（n∈N*）上的最大值与最小值；
（3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
①f（2-n）与2-n+2（n∈N*）；
②f（x）与2x+2（x∈（0，1]）．
（2013•黄埔区一模）已知集合A={x|0＜x＜3}，B={x|x2≥4}，则A∩B=
{x|2≤x＜3}
{x|2≤x＜3}
．
（2013•黄埔区一模）已知tanα=
1
2
，tan(β-α)=-
1
3
，则tan（β-2α）的值为
-1
-1
．
（2013•黄埔区一模）已知命题“若f（x）=m2x2，g（x）=mx2-2m，则集合{x|f(x)＜g(x)，
12
≤x≤1}=∅”是假命题，则实数m的取值范围是
（-7，0）
（-7，0）
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网