题目内容
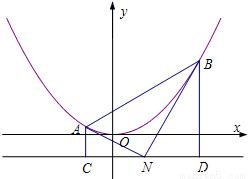
 如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.
如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.求证:直线AB必经过y轴上的一个定点Q,并写出点Q的坐标.
分析:设点N,A,B的坐标代入抛物线方程,求得y=
,求导数后可知切线斜率进而可得
=
,化简整理得x12-2mx1-4p2=0,同理可得x22-2mx2-4p2=0,进而可知x1和x2是关于x的方程x2-2mx-4p2=0的两个根,进而可求得这两个根,直线AB的方程y-y1=
(x-x1)中,令x=0得y=y1-
x1=
整理后可知结果为定值,进而可知直线AB必经过y轴上的一个定点Q(0,p),即抛物线的焦点.
| x2 |
| 4p |
| y1+p |
| x1-m |
| x1 |
| 2p |
| y2-y1 |
| x2-x1 |
| y2-y1 |
| x2-x1 |
| x2y1-x1y2 |
| x2-x1 |
解答:证明:因为抛物线的准线l的方程为y=-p,
所以可设点N,A,B的坐标分别为(m,-p),(x1,y1),(x2,y2),
则x12=4py1,x22=4py2,由x2=4py,得y=
,
求导数得y′=
,于是
=
,
即
=
,
化简得x12-2mx1-4p2=0,
同理可得x22-2mx2-4p2=0,
所以x1和x2是关于x的方程x2-2mx-4p2=0
两个实数根,所以x1,2=m±
,且x1x2=-4p2.
在直线AB的方程y-y1=
(x-x1)中,
令x=0,
得y=y1-
x1=
═
=-
=p为定值,
所以直线AB必经过y轴上的一个定点Q(0,p),即抛物线的焦点.
所以可设点N,A,B的坐标分别为(m,-p),(x1,y1),(x2,y2),
则x12=4py1,x22=4py2,由x2=4py,得y=
| x2 |
| 4p |
求导数得y′=
| x |
| 2p |
| y1+p |
| x1-m |
| x1 |
| 2p |
即
| ||||
| x1-m |
| x1 |
| 2p |
化简得x12-2mx1-4p2=0,
同理可得x22-2mx2-4p2=0,
所以x1和x2是关于x的方程x2-2mx-4p2=0
两个实数根,所以x1,2=m±
| m2+4p2 |
在直线AB的方程y-y1=
| y2-y1 |
| x2-x1 |
令x=0,
得y=y1-
| y2-y1 |
| x2-x1 |
| x2y1-x1y2 |
| x2-x1 |
| x1x2(x1-x2) |
| 4p(x2-x1) |
| x1x2 |
| 4p |
所以直线AB必经过y轴上的一个定点Q(0,p),即抛物线的焦点.
点评:本题主要考查了抛物线的应用,考查了学生综合分析问题和运算的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
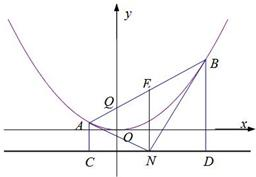
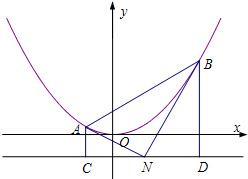 如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.
如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.