题目内容
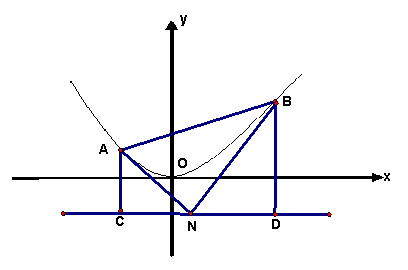
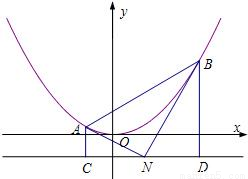
 如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.
如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.(1)求证:直线AB必经过y轴上的一个定点Q,并写出点Q的坐标;
(2)若△ACN,△BDN,△ANB的面积依次构成等差数列,求此时点N的坐标.
分析:(1)因为抛物线的准线l的方程为y=-p,所以可设点N,A,B的坐标分别为(m,-p),(x1,y1),(x2,y2),由题设条件知x12-2mx1-4p2=0,x22-2mx2-4p2=0,所以x1和x2是关于x的方程x2-2mx-4p2=0两个实数根,所以x1,2=m±
,由此可知直线AB必经过y轴上的一个定点Q(0,p),即抛物线的焦点.
(2)由(1)知x1+x2=2m,所以N为线段CD的中点,取线段AB的中点E,因为Q是抛物线的焦点,所以AQ=AC,BQ=BD,所以AC+BD=AB,
所以S△ANB=S△ANE+S△BNE=
EN•CN+
EN•DN=
EN•(CN+DN)=EN•CN=
•CN=
,又因为S△ACN=
=
,S△BDN=
=
,所以
,
,
成等差数列,即AQ,BQ,AB成等差数列,由此入手可求出点N的坐标.
| m2+4p2 |
(2)由(1)知x1+x2=2m,所以N为线段CD的中点,取线段AB的中点E,因为Q是抛物线的焦点,所以AQ=AC,BQ=BD,所以AC+BD=AB,
所以S△ANB=S△ANE+S△BNE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC+BD |
| 2 |
| AB•CN |
| 2 |
| AC•CN |
| 2 |
| AQ•CN |
| 2 |
| BD•DN |
| 2 |
| BQ•CN |
| 2 |
| AQ•CN |
| 2 |
| BQ•CN |
| 2 |
| AB•CN |
| 2 |
解答:解:(1)因为抛物线的准线l的方程为y=-p,所以可设点N,A,B的坐标分别为(m,-p),(x1,y1),(x2,y2),则x12=4py1,x22=4py2,由x2=4py,得y=
,求导数得y′=
,于是
=
,即
=
,
化简得x12-2mx1-4p2=0,
同理可得x22-2mx2-4p2=0,
所以x1和x2是关于x的方程x2-2mx-4p2=0
两个实数根,所以x1,2=m±
,且x1x2=-4p2.
在直线AB的方程y-y1=
(x-x1)中,
令x=0,
得y=y1-
x1=
═
=-
=p为定值,
所以直线AB必经过y轴上的一个定点Q(0,p),即抛物线的焦点.(5分)
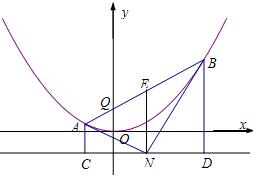
(2)由(1)知x1+x2=2m,所以N为线段CD的中点,取线段AB的中点E,
因为Q是抛物线的焦点,所以AQ=AC,BQ=BD,所以AC+BD=AB,
所以S△ANB=S△ANE+S△BNE=
EN•CN+
EN•DN=
EN•(CN+DN)=EN•CN=
•CN=
,
又因为S△ACN=
=
,S△BDN=
=
,
所以
,
,
成等差数列,即AQ,BQ,AB成等差数列,
即0-x1,x2-0,x2-x1成等差数列,所以x2-2x1=2x2,x2=-2x1,
所以x1x2=-2
=(m+
)(m-
)=-4p2,x1=±
p,x1=
p时,x2=-2
p,m=
=-
p,x1=-
p时,x2=2
p,m=
=
p,所以所求点N的坐标为(±
p, -p).
(10分)
| x2 |
| 4p |
| x |
| 2p |
| y1+p |
| x1-m |
| x1 |
| 2p |
| ||||
| x1-m |
| x1 |
| 2p |
化简得x12-2mx1-4p2=0,
同理可得x22-2mx2-4p2=0,
所以x1和x2是关于x的方程x2-2mx-4p2=0
两个实数根,所以x1,2=m±
| m2+4p2 |
在直线AB的方程y-y1=
| y2-y1 |
| x2-x1 |
令x=0,
得y=y1-
| y2-y1 |
| x2-x1 |
| x2y1-x1y2 |
| x2-x1 |
| x1x2(x1-x2) |
| 4p(x2-x1) |
| x1x2 |
| 4p |
所以直线AB必经过y轴上的一个定点Q(0,p),即抛物线的焦点.(5分)
(2)由(1)知x1+x2=2m,所以N为线段CD的中点,取线段AB的中点E,
因为Q是抛物线的焦点,所以AQ=AC,BQ=BD,所以AC+BD=AB,
所以S△ANB=S△ANE+S△BNE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC+BD |
| 2 |
| AB•CN |
| 2 |
又因为S△ACN=
| AC•CN |
| 2 |
| AQ•CN |
| 2 |
| BD•DN |
| 2 |
| BQ•CN |
| 2 |
所以
| AQ•CN |
| 2 |
| BQ•CN |
| 2 |
| AB•CN |
| 2 |
即0-x1,x2-0,x2-x1成等差数列,所以x2-2x1=2x2,x2=-2x1,
所以x1x2=-2
| x | 2 1 |
| m2+4p2 |
| m2+4p2 |
| 2 |
| 2 |
| 2 |
| x1+x2 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| x1+x2 |
| 2 |
| ||
| 2 |
| ||
| 2 |

(10分)
点评:本题考查直线和圆锥曲线的位置关系,数形结合效果很好.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
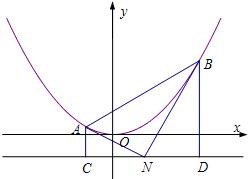
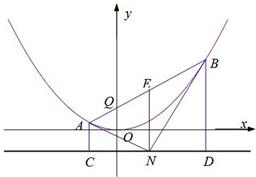 如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.
如图,已知抛物线M:x2=4py(p>0)的准线为l,N为l上的一个动点,过点N作抛物线M的两条切线,切点分别为A,B,再分别过A,B两点作l的垂线,垂足分别为C,D.