题目内容
（本题满分10分）
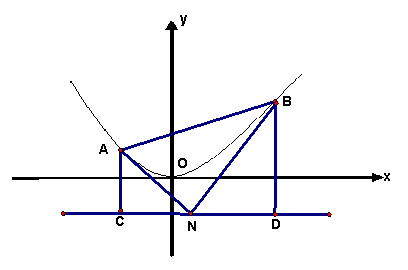
如图，已知抛物线M：
的准线为
，N为上的一个动点，过点N作抛物线M的两条切线，切点分别为A、B，再分别过A、B两点作的垂线，垂足分别为C，D。
求证：直线AB必经过y轴上的一个定点Q，并写出点Q的坐标；
若
的面积成等差数列，求此时点N的坐标。
【必做题】
解法一：（1）因为抛物线的准线
的方程为
，
所以可设点
的坐标分别为
，
，
，则
，
，
由
，得
，求导数得
，于是
，
即
，化简得
，
同理可得
，
所以
和
是关于
的方程
两个实数根，所以
，
且
．
在直线
的方程
中，
令
，得
=
为定值，
所以直线必经过
轴上的一个定点
，即抛物线的焦点．……………………………5分
(2)由（1）知
，所以
为线段
的中点，取线段的中点
，
因为
是抛物线的焦点，所以
，所以
，
所以
，
又因为
，
，
所以
，
，
成等差数列，即
成等差数列，
即
成等差数列，所以
，
，
所以
，
，
时，
，
，
时，
，
，
所以所求点
的坐标为
．………………………………………………………………10分
解法二：（1）因为已知抛物线的准线的方程为，所以可设点
的坐标分别为，，，则，，
设过点与抛物线相切的直线方程为
，与抛物线方程
联立，消去得
，
因为直线与抛物线相切，所以
，即
，解得
，此时两切点横坐标分别为
，
在直线的方程中，令得
=为定值，
所以直线必经过轴上的一个定点，即抛物线的焦点．……………………………5分
（2）由（1）知两切线的斜率分别为，则
，所以
，
连接
，则直线斜率为
，
又因为直线的斜率
，
所以
，
所以
，又因为，所以
，
所以
和
的面积成等差数列，所以成等差数列，
所以成等差数列，所以，，
所以，，
时，，，
时，，
，
所以所求点的坐标为
． …………………………………………………………10分
（以上各题如考生另有解法，请参照本评分标准给分）
练习册系列答案
相关题目
的图象在y轴上的截距为
，相邻的两个最值点是
和
（1）求函数
；（2）设
，问将函数
的图像？（3）画出函数
上的简图．
，求证：
；
，求证：三数
，
，
中至少有一个不小于2.
的所有棱长都为2，
为棱
的中点，
平面
；
的余弦值大小.
与
的距离，由于地形的限制，需要在岸上选取
和
两点，现测得
，
，
，
，
，求两景点