Question

【题目】已知是等差数列，，是等比数列，，，，.

（1）求数列的通项公式；

（2）若，求当是偶数时，数列的前项和；

（3）若，是否存在实数使得不等式对任意的，恒成立？若存在，求出所有满足条件的实数，若不存在，请说明理由.

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）设数列的公差为，数列的公比为，由得，从而有，解方程组即可求出答案；

（2）由（1）可得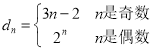，利用分组求和法即可求出答案；

（3）由（1）得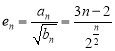，，由邻项比较法可求得，由辅助角公式可求得，由此可求出答案．

解：（1）设数列的公差为，数列的公比为，

∵，，，

∴，得，

又，，

∴，解得，

∴，

，

∴；

（2）由（1）可得，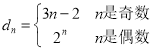

当是偶数时，

；

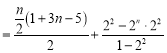
（3）由（1）得，，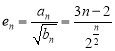

由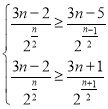，解得，

∵，

∴当时，有，

∵，

∴，

若不等式对任意的，恒成立，

则，

∴存在实数满足条件．