题目内容
在直角坐标系xOy中,直线y=2x- 与圆x2+y2=1交于A,B两点,记∠xOA=α(0<α<
与圆x2+y2=1交于A,B两点,记∠xOA=α(0<α< ),∠xOB=β(π<β<
),∠xOB=β(π<β< ),则sin(α+β)的值为
),则sin(α+β)的值为
- A.

- B.

- C.-

- D.-

D
分析:把直线与圆的方程联立得到关于x与y的二元二次方程组,求出方程组的解即可得到交点A和B的坐标,然后根据α为第一象限的角,由点A的坐标分别求出sinα和cosα的值,β为第三象限的角,由点B的坐标分别求出sinβ和cosβ的值,最后把所求的式子利用两角和的正弦函数公式化简后,将各自的值代入即可求出值.
解答:联立得: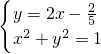
解得: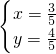 或
或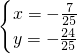
所以点A( ,
, ),点B(-
),点B(- ,-
,- ).
).
由∠xOA=α为第一象限的角,∠xOB=β为第三象限的角,
根据两点的坐标分别得到:
sinα= ,cosα=
,cosα= ,sinβ=-
,sinβ=- ,cosβ=-
,cosβ=- ,
,
则sin(α+β)=sinαcosβ+cosαsinβ= ×(-
×(- )+
)+ ×(-
×(- )=-
)=- .
.
故选D
点评:此题考查学生掌握象限角的三角函数值的求法,灵活运用两角和的正弦函数公式化简求值,是一道中档题.
分析:把直线与圆的方程联立得到关于x与y的二元二次方程组,求出方程组的解即可得到交点A和B的坐标,然后根据α为第一象限的角,由点A的坐标分别求出sinα和cosα的值,β为第三象限的角,由点B的坐标分别求出sinβ和cosβ的值,最后把所求的式子利用两角和的正弦函数公式化简后,将各自的值代入即可求出值.
解答:联立得:
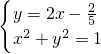
解得:
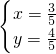 或
或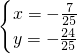
所以点A(
 ,
, ),点B(-
),点B(- ,-
,- ).
).由∠xOA=α为第一象限的角,∠xOB=β为第三象限的角,
根据两点的坐标分别得到:
sinα=
 ,cosα=
,cosα= ,sinβ=-
,sinβ=- ,cosβ=-
,cosβ=- ,
,则sin(α+β)=sinαcosβ+cosαsinβ=
 ×(-
×(- )+
)+ ×(-
×(- )=-
)=- .
.故选D
点评:此题考查学生掌握象限角的三角函数值的求法,灵活运用两角和的正弦函数公式化简求值,是一道中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为