题目内容
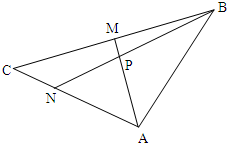 如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),点N在AC上,且
如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),点N在AC上,且| AN |
| NC |
(1)点P分向量
| AM |
(2)P点坐标.
分析:由定比分点坐标公式求出M、N、P的坐标,进而求出
与
的坐标,由
与
共线可得有
×
-
×
=0,解之得λ=4,从而得到点P的坐标.
| BP |
| BN |
| BP |
| BN |
| -3-4λ |
| 1+λ |
| -8 |
| 3 |
| -4-λ |
| 1+λ |
| -19 |
| 3 |
解答:解:(1)∵A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),
由于M为BC中点,可得M点的坐标为(1,1).…(2分)
由
=2
可得N点的坐标为 (-
,-
). …(4分)
又由
=λ
可得P点的坐标为(
,
),
从而得
=(
,
),
=(
,
).
∵
与
共线,故有
×
-
×
=0,解之得λ=4. …(8分)
∴点P的坐标为(
,
). …(12分)
由于M为BC中点,可得M点的坐标为(1,1).…(2分)
由
| AN |
| NC |
| 4 |
| 3 |
| 2 |
| 3 |
又由
| AP |
| PM |
| 2+λ |
| 1+λ |
| -2+λ |
| 1+λ |
从而得
| BP |
| -3-4λ |
| 1+λ |
| -4-λ |
| 1+λ |
| BN |
| -19 |
| 3 |
| -8 |
| 3 |
∵
| BP |
| BN |
| -3-4λ |
| 1+λ |
| -8 |
| 3 |
| -4-λ |
| 1+λ |
| -19 |
| 3 |
∴点P的坐标为(
| 6 |
| 5 |
| 2 |
| 5 |
点评:本题主要考查线段的定比分点分有向线段成的比的定义,及定比分点坐标公式,本题主要考查两个向量共线的性质,两个向量坐标形式的运算,属于基础题.

练习册系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知