题目内容
为迎接我校110周年校庆,校友会于日前举办了一次募捐爱心演出,有1000 人参加,每人一张门票,每张100元. 在演出过程中穿插抽奖活动.第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 ,满足
,满足 电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
(1)已知校友甲在第一轮抽奖中被抽中,求校友甲在第二轮抽奖中获奖的概率;
(2)若校友乙参加了此次活动,求校友乙参加此次活动收益的期望;
 ,满足
,满足 电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.(1)已知校友甲在第一轮抽奖中被抽中,求校友甲在第二轮抽奖中获奖的概率;
(2)若校友乙参加了此次活动,求校友乙参加此次活动收益的期望;
(Ⅰ)P(A)=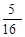 ;(Ⅱ)
;(Ⅱ)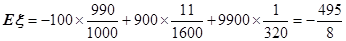
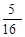 ;(Ⅱ)
;(Ⅱ)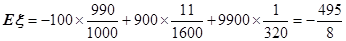
本题考查离散型随机变量的概率分布列与期望,解题的关键是明确变量的可能取值及其含义.
(Ⅰ)确定从0,1,2,3四个数字中有重复取2个数字的基本事件的个数,与校友甲在第二轮抽奖中获奖的基本事件个数,即可求得校友甲在第二轮抽奖中获奖的概率;(Ⅱ)设校友乙参加此次活动的收益为ξ,ξ的可能取值为-100,900,9900,求出相应的概率,即可得到分布列与数学期望.
17. 解:(Ⅰ)从0,1,2,3四个数字中有重复取2个数字,其基本事件有
(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)共 16 个………………………………………………………………………………3分
设“校友甲在第二轮抽奖中获奖”为事件A,且事件A所包含的基本事件有
(0,0),(2,0),(3,0),(3,1),(3,3)共5个,
∴P(A)=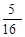 ……………………………………………………………………………6分
……………………………………………………………………………6分
(Ⅱ)设校友乙参加此次活动的收益为ξ,ξ的可能取值为-100,900,9900.
P(ξ=-100)=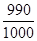 ,P(ξ=900)=
,P(ξ=900)=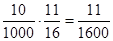 ,
,
P(ξ="9900)="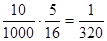 …………………………………………………9分
…………………………………………………9分
∴ξ的分布列为
∴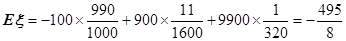 ………………12分
………………12分
(Ⅰ)确定从0,1,2,3四个数字中有重复取2个数字的基本事件的个数,与校友甲在第二轮抽奖中获奖的基本事件个数,即可求得校友甲在第二轮抽奖中获奖的概率;(Ⅱ)设校友乙参加此次活动的收益为ξ,ξ的可能取值为-100,900,9900,求出相应的概率,即可得到分布列与数学期望.
17. 解:(Ⅰ)从0,1,2,3四个数字中有重复取2个数字,其基本事件有
(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)共 16 个………………………………………………………………………………3分
设“校友甲在第二轮抽奖中获奖”为事件A,且事件A所包含的基本事件有
(0,0),(2,0),(3,0),(3,1),(3,3)共5个,
∴P(A)=
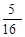 ……………………………………………………………………………6分
……………………………………………………………………………6分(Ⅱ)设校友乙参加此次活动的收益为ξ,ξ的可能取值为-100,900,9900.
P(ξ=-100)=
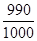 ,P(ξ=900)=
,P(ξ=900)=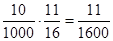 ,
,P(ξ="9900)="
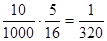 …………………………………………………9分
…………………………………………………9分∴ξ的分布列为
| ξ | -100 | 900 | 9900 |
| P | 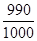 | 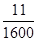 | 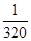 |
∴
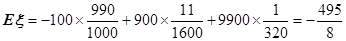 ………………12分
………………12分
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率; .
. 为在体操岗位服务的美国志愿者的个数,求
为在体操岗位服务的美国志愿者的个数,求 (
( 、
、 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表: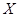 ,求
,求 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为 ,试写出
,试写出 四个不同的岗位服务,每个岗位至少有一名志愿者,设随机变量
四个不同的岗位服务,每个岗位至少有一名志愿者,设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,则
岗位服务的人数,则 _
_ 的概率分布列如下,且
的概率分布列如下,且 则
则