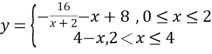题目内容
【题目】选修4—5:不等式选讲
设![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题本题主要考查绝对值不等式的解法、恒成立问题、函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,将![]() 代入,利用零点分段法去掉绝对值符号解不等式;第二问,将
代入,利用零点分段法去掉绝对值符号解不等式;第二问,将![]() 对于
对于![]() 恒成立,转化为
恒成立,转化为![]() 对于
对于![]() 恒成立,先将
恒成立,先将![]() 转化为分段函数,结合图象求出函数
转化为分段函数,结合图象求出函数![]() 的最小值,代入到
的最小值,代入到![]() 中,即解出m的取值范围.
中,即解出m的取值范围.
试题解析:(1)当![]() 时,
时,![]() ,
,
不等式![]() 为
为![]() ,
,
①当![]() 时,不等式为:
时,不等式为:![]() ,即
,即![]() ,满足;
,满足;
②当![]() 时,不等式为:
时,不等式为:![]() ,即
,即![]() ,不满足;
,不满足;
③当![]() 时,不等式为:
时,不等式为:![]() ,即
,即![]() ,满足.
,满足.
综上所述,不等式![]() 的解集为
的解集为![]() .
.
(2)设![]() ,若
,若![]() 对于
对于![]() 恒成立,
恒成立,
即![]() 对于
对于![]() 恒成立,
恒成立,
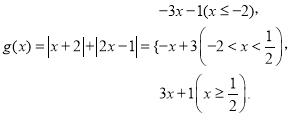
由图可看出![]() 的最小值是
的最小值是![]() ,
,
所以![]() ,
,![]() ,即m的取值范围是
,即m的取值范围是![]() .
.


练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目