题目内容
将B=| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
①AC⊥MN ②DM与平面ABC所成角为θ ③线段MN的最大值是
| 3 |
| 4 |
| ||
| 4 |
| π |
| 2 |
| π |
| 2 |
分析:根据菱形的性质以及翻折后一些量之间的关系可得①正确;由题意可得∠BMD=θ,并且得到∠BMD为DM与平面ABC所成角,所以②正确;根据题意折后两条对角线AC、BD之间的距离为NM的长,再根据解三角形的有关知识可得答案③正确;根据条件可得:BC⊥平面ACD,这与BM⊥平面ACD相矛盾,所以④错误.
解答:解:翻折后如图所示:
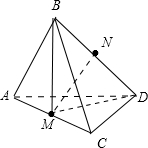
因为BM⊥AC,DM⊥AC,所以AC⊥平面BMD,所以AC⊥MN.
所以①正确.
因为AC⊥平面BMD,
所以AC⊥BM,AC⊥DM,并且平面BMD⊥平面ABC,
所以∠BMD=θ,∠BMD为DM与平面ABC所成角,
所以DM与平面ABC所成角为θ.
所以②正确.
又因为BM=DM,
所以MN⊥BD.
所以折后两条对角线AC、BD之间的距离为NM的长,
在△BMD中,∠BMD=θ,BM=DM=
,
当θ=
时,MN的最小值为
,
当θ=
时,MN的最大值为
.
所以③正确.
因为当θ=
时,则有∠BMD=90°,
所以BM⊥平面ACD,MD⊥平面ABC,
所以MD⊥BC.
若BC与AD所成角等于
,即BC⊥AD,
所以BC⊥平面ACD,
这与BM⊥平面ACD相矛盾.
所以④错误.
故答案为①②③.

因为BM⊥AC,DM⊥AC,所以AC⊥平面BMD,所以AC⊥MN.
所以①正确.
因为AC⊥平面BMD,
所以AC⊥BM,AC⊥DM,并且平面BMD⊥平面ABC,
所以∠BMD=θ,∠BMD为DM与平面ABC所成角,
所以DM与平面ABC所成角为θ.
所以②正确.
又因为BM=DM,
所以MN⊥BD.
所以折后两条对角线AC、BD之间的距离为NM的长,
在△BMD中,∠BMD=θ,BM=DM=
| ||
| 2 |
当θ=
| 2π |
| 3 |
| ||
| 4 |
当θ=
| π |
| 3 |
| 3 |
| 4 |
所以③正确.
因为当θ=
| π |
| 2 |
所以BM⊥平面ACD,MD⊥平面ABC,
所以MD⊥BC.
若BC与AD所成角等于
| π |
| 2 |
所以BC⊥平面ACD,
这与BM⊥平面ACD相矛盾.
所以④错误.
故答案为①②③.
点评:本题主要考查二面角、线面角问题,解决此类问题一般先作出空间角,再通过解三角形的有关知识解决问题,本题并且也考查了异面直线的夹角与距离问题,此题属于中档题型.

练习册系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折起,使得点A到点A′的位置,且A′C=1,则折起后二面角A′-DC-B的大小( )
A、arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
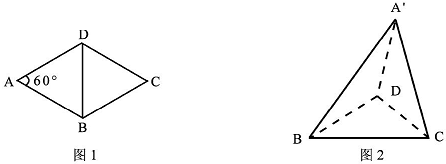 (2013•凉山州二模)图1是边长为1的菱形,∠DAB=60°,现沿BD将△ABD翻折起,得四面体A′-BDC(图2),若二面角A′-BD-C的平面角为α(0<a<π),给出以下四个命题:
(2013•凉山州二模)图1是边长为1的菱形,∠DAB=60°,现沿BD将△ABD翻折起,得四面体A′-BDC(图2),若二面角A′-BD-C的平面角为α(0<a<π),给出以下四个命题: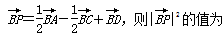
 D.9/4
D.9/4