题目内容
已知数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0(n∈N*).
(Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)设Tn=|a1|+|a2|+|a3|+…+|an|,求T10.
(Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)设Tn=|a1|+|a2|+|a3|+…+|an|,求T10.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(I)由已知得{an}是首项为8,公差为-2的等差数列,由此能求出数列{an}的通项公式及前n项和Sn.
(Ⅱ)由an=10-2n,得当n>5时,an<0;当n=5时,an=0;当n<5时,an>0.由此能求出T10=2S5-S10=50.
(Ⅱ)由an=10-2n,得当n>5时,an<0;当n=5时,an=0;当n<5时,an>0.由此能求出T10=2S5-S10=50.
解答:
解:(I)∵an+2-2an+1+an=0.
∴an+2-an+1=an+1-an=…=a2-a1,
∴{an}是等差数列,…(2分)
且a1=8,a4=2,∴d=-2,…(3分)
an=a1+(n-1)d=10-2n.…(4分)
Sn=na1+
d=8n-n(n-1)=-n2+9n.…(6分)
(Ⅱ)∵an=10-2n,令an=0,得n=5,
当n>5时,an<0;当n=5时,an=0;
当n<5时,an>0,
∴T10=|a1|+|a2|+|a3|+…+|a10|
=S5-(S10-S5)
=2S5-S10
=2(-25+45)-(-100+90)
=50.
∴an+2-an+1=an+1-an=…=a2-a1,
∴{an}是等差数列,…(2分)
且a1=8,a4=2,∴d=-2,…(3分)
an=a1+(n-1)d=10-2n.…(4分)
Sn=na1+
| n(n-1) |
| 2 |
(Ⅱ)∵an=10-2n,令an=0,得n=5,
当n>5时,an<0;当n=5时,an=0;
当n<5时,an>0,
∴T10=|a1|+|a2|+|a3|+…+|a10|
=S5-(S10-S5)
=2S5-S10
=2(-25+45)-(-100+90)
=50.
点评:本题考查数列的通项公式和前n项和公式的求法,考查数列的前10项的绝对值的和的求法,是中档题,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
若直线(1+a)x+y-1=0与圆x2+y2+4x=0相切,则a的值为( )
| A、1或-1 | ||||
B、
| ||||
| C、1 | ||||
D、-
|
下列函数中,增长速度最快的是( )
| A、y=20x |
| B、y=x20 |
| C、y=log20x |
| D、y=20x |
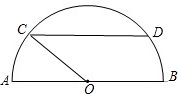 如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧