题目内容
已知双曲线C:
-
=1(a>0,b>0)的左、右焦点分别F1、F2,O为双曲线的中心,P是双曲线右支上异于顶点的任一点,△PF1F2的内切圆的圆心为I,且⊙I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,若e为双曲线的离心率,下面八个命题:
①△PF1F2的内切圆的圆心在直线x=b上;
②△PF1F2的内切圆的圆心在直线x=a上;
③△PF1F2的内切圆的圆心在直线OP上;
④△PF1F2的内切圆必通过点(a,0);
⑤|OB|=e|OA|;
⑥|OB|=|OA|;
⑦|OA|=e|OB|;
⑧|OA|与|OB|关系不确定.
其中正确的命题的代号是
| x2 |
| a2 |
| y2 |
| b2 |
①△PF1F2的内切圆的圆心在直线x=b上;
②△PF1F2的内切圆的圆心在直线x=a上;
③△PF1F2的内切圆的圆心在直线OP上;
④△PF1F2的内切圆必通过点(a,0);
⑤|OB|=e|OA|;
⑥|OB|=|OA|;
⑦|OA|=e|OB|;
⑧|OA|与|OB|关系不确定.
其中正确的命题的代号是
②,④,⑥
②,④,⑥
.分析:利用切线长定理,结合双曲线的定义,把|PF1|-|PF2|=2a,转化为|AF1|-|AF2|=2a,从而求得点A的横坐标.再在三角形PCF2中,由题意得,它是一个等腰三角形,从而在三角形F1CF2中,利用中位线定理得出OB,从而解决问题.
解答: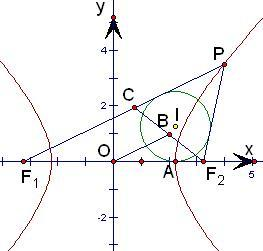 解:根据题意得F1(-c,0)、F2(c,0),
解:根据题意得F1(-c,0)、F2(c,0),
设△PF1F2的内切圆分别与PF1、PF2切于点A1、B1,与F1F2切于点A,
则|PA1|=|PB1|,|F1A1|=|F1A|,|F2B1|=|F2A|,
又点P在双曲线右支上,
所以|PF1|-|PF2|=2a,故|F1A|-|F2A|=2a,而|F1A|+|F2A|=2c,
设A点坐标为(x,0),
则由|F1A|-|F2A|=2a可得(x+c)-(c-x)=2a
解得x=a,则△PF1F2的内切圆必通过点(a,0),△PF1F2的内切圆的圆心在直线x=a上,
故②,④正确.
由于|OA|=a,在三角形PCF2中,由题意得,三角形PCF2是一个等腰三角形,PC=PF2,
∴在三角形F1CF2中,有:
OB=
CF1=
(PF1-PC)=
(PF1-PF2)=
×2a=a.
∴|OB|=|OA|.⑥正确.
故答案为:②,④,⑥.
 解:根据题意得F1(-c,0)、F2(c,0),
解:根据题意得F1(-c,0)、F2(c,0),设△PF1F2的内切圆分别与PF1、PF2切于点A1、B1,与F1F2切于点A,
则|PA1|=|PB1|,|F1A1|=|F1A|,|F2B1|=|F2A|,
又点P在双曲线右支上,
所以|PF1|-|PF2|=2a,故|F1A|-|F2A|=2a,而|F1A|+|F2A|=2c,
设A点坐标为(x,0),
则由|F1A|-|F2A|=2a可得(x+c)-(c-x)=2a
解得x=a,则△PF1F2的内切圆必通过点(a,0),△PF1F2的内切圆的圆心在直线x=a上,
故②,④正确.
由于|OA|=a,在三角形PCF2中,由题意得,三角形PCF2是一个等腰三角形,PC=PF2,
∴在三角形F1CF2中,有:
OB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|OB|=|OA|.⑥正确.
故答案为:②,④,⑥.
点评:本题考查双曲线的定义、切线长定理.解答的关键是充分利用平面几何的性质,如三角形内心的性质等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目