题目内容
15.函数f(x)=sinx+cosx(x∈R)的图象向右平移了m个单位后,得到函数y=f′(x)的图象,其中m∈(0,2π),则m的值是$\frac{3π}{2}$.分析 f(x)=sinx+cosx=$\sqrt{2}sin(x+\frac{π}{4})$,y=f′(x)=cosx-sinx=$\sqrt{2}$$sin(x+\frac{3π}{4})$,根据把f(x)图象向右平移了m个单位后,得到函数y=f′(x)的图象,其中m∈(0,2π),可得$\sqrt{2}sin(x+\frac{π}{4}-m)$=$\sqrt{2}$$sin(x+\frac{3π}{4})$,解出即可得出.
解答 解:f(x)=sinx+cosx=$\sqrt{2}(\frac{\sqrt{2}}{2}sinx+\frac{\sqrt{2}}{2}cosx)$=$\sqrt{2}sin(x+\frac{π}{4})$,
y=f′(x)=cosx-sinx=-$\sqrt{2}$$sin(x-\frac{π}{4})$=$\sqrt{2}$$sin(x+\frac{3π}{4})$,
∵把f(x)图象向右平移了m个单位后,得到函数y=f′(x)的图象,其中m∈(0,2π),
∴$\sqrt{2}sin(x+\frac{π}{4}-m)$=$\sqrt{2}$$sin(x+\frac{3π}{4})$,
∴$x+\frac{π}{4}-m$=2kπ+π-$(x+\frac{3π}{4})$(舍去),或$2kπ+x+\frac{3π}{4}$,
∴m=$-2kπ-\frac{π}{2}$,取k=-1,
则m=$\frac{3π}{2}$.
故答案为:$\frac{3π}{2}$.
点评 本题考查了和差公式、图象变换、导数运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.如图,在棱长为3的正方体ABCD-A1B1C1D1中,点C1到平面A1BD的距离为( )
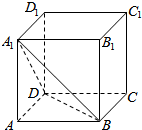

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
5.方程|x|+|y|=1表示的曲线是( )
| A. |  | B. | 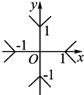 | C. | 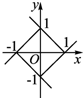 | D. | 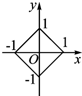 |