题目内容
10.设函数f(x)=ex+g(x).若曲线y=g(x)在点P(0,g(0))处的切线方程是y=2x+1,则曲线y=f(x)在点Q(0,f(0))处的切线方程是( )| A. | y=2x+1 | B. | y=2x+3 | C. | y=x+2 | D. | y=3x+2 |
分析 由题意,g′(0)=2,g(0)=1,可得f′(0)=e0+g′(0)=3,f(0)=2,即可求出曲线y=f(x)在点Q(0,f(0))处的切线方程.
解答 解:由题意,g′(0)=2,g(0)=1,
∴f′(0)=e0+g′(0)=3,f(0)=2,
∴曲线y=f(x)在点Q(0,f(0))处的切线方程是y=3x+2.
故选:D.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查学生的计算能力,比较基础.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2.等差数列{an}中,已知a1+a4+a7=39,a3+a6+a9=27,求a2+a8=( )
| A. | 11 | B. | 22 | C. | 33 | D. | 44 |
19.函数f(x)=tanωx(ω>0)的图象的相邻两个零点的距离为$\frac{π}{2}$,则$f(\frac{π}{6})$的值是( )
| A. | -$\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | 1 |
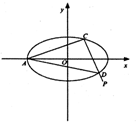 如图,在平面直角坐标系xOy中,A是椭圆G:$\frac{{x}^{2}}{4}$+y2=1的左顶点,过点P(2,-1)任意作一条直线l与椭圆G交于C,D,记直线AC,AD的斜率分别为k1,k2,则$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$的值为-4.
如图,在平面直角坐标系xOy中,A是椭圆G:$\frac{{x}^{2}}{4}$+y2=1的左顶点,过点P(2,-1)任意作一条直线l与椭圆G交于C,D,记直线AC,AD的斜率分别为k1,k2,则$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$的值为-4.