题目内容
14. 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥AD于O,AP⊥BC,已知BC=8,PO=4,AO=3,OD=2.
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥AD于O,AP⊥BC,已知BC=8,PO=4,AO=3,OD=2.(1)证明:PO⊥平面ABC;
(2)在线段AP上是否存在点M,使得二面角A-MC-B的大小为π4π4?若存在,求出AM的长;若不存在,请说明理由.
分析 (1)证明BC⊥平面PAD,可得BC⊥PO,结合PO⊥AD,BC∩AD=D,证明PO⊥平面ABC;
(2)以O为原点,以AD方向为Y轴正方向,以射线OP的方向为Z轴正方向,建立空间坐标系,求平面BMC和平面AMC的法向量,利用向量的夹角公式,即可得出结论.
解答 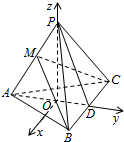 解:(1)∵AB=AC,D为BC的中点,
解:(1)∵AB=AC,D为BC的中点,
∴BC⊥AD,
∵AP⊥BC,AD∩AP=A,
∴BC⊥平面PAD,
∵PO?平面PAD,
∴BC⊥PO,
∵PO⊥AD,BC∩AD=D,
∴PO⊥平面ABC;
(2)以O为原点,以AD方向为Y轴正方向,以射线OP的方向为Z轴正方向,建立空间坐标系,则O(0,0,0),A(0,-3,0),B(4,2,0),C(-4,2,0),P(0,0,4)
设→PM−−→PM=λ→PA−−→PA,λ≠1,则→PM−−→PM=λ(0,-3,-4),→BM−−→BM=(-4,-2,4)+λ(0,-3,-4)=(-4,-2-3λ,4-4λ)
∵→BC−−→BC=(-8,0,0)
∴设平面BMC的法向量→m→m=(a,b,c)
则{−4a−(2+3λ)b+(4−4λ)c=0−8a=0
令b=1,则→m=(0,1,2+3λ4−4λ)
平面AMC的法向量→n=(x,y,z),
∵→AC=(-4,5,0),→AM=→AB+→BM=(0,3-3λ,4-4λ)
∴{−4x+5y=0(3−3λ)y+(4−4λ)z=0
令x=5,则→n=(5,4,-3)
由二面角A-MC-B的大小为π4,得√22=4−6+9λ4−4λ√1+(2+3λ4−4λ)2•√50
∴456λ2-240λ+400=0,
方程无解,∴不存在点M使得二面角A-MC-B的大小为π4.
点评 本题考查的知识点是线面垂直的判定,与二面角有关的立体几何综合题,其中建立空间坐标系,求出平面的法向量是解答本题的关键.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | {1} | B. | {2,4} | C. | {2,3} | D. | (1,4) |
 为了解某地高中生身高情况,研究小组在该地高中生中随机抽取30名高中生的身高编成如图所示的茎叶图(单位:cm);若身高在175cm以上(包括175cm)定义为“高个子”,身高在175以下(不包括175cm)定义为“非高个子”.
为了解某地高中生身高情况,研究小组在该地高中生中随机抽取30名高中生的身高编成如图所示的茎叶图(单位:cm);若身高在175cm以上(包括175cm)定义为“高个子”,身高在175以下(不包括175cm)定义为“非高个子”. 某校在2014年对2000名高一新生进行英语特长测试选拔,现抽取部分学生的英语成绩,将所得数据整理后得出频率分布直方图如图所示,图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
某校在2014年对2000名高一新生进行英语特长测试选拔,现抽取部分学生的英语成绩,将所得数据整理后得出频率分布直方图如图所示,图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.