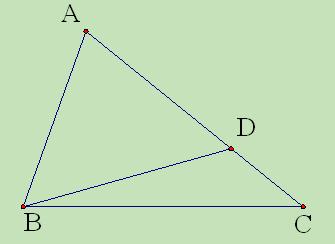
题目内容
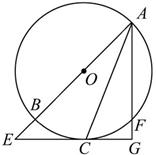
如图,直线 过圆心
过圆心 ,交⊙
,交⊙ 于
于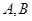 ,直线
,直线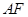 交⊙
交⊙ 于
于 (不与
(不与 重合),直线
重合),直线 与⊙
与⊙ 相切于
相切于 ,交
,交 于
于 ,且与
,且与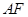 垂直,垂足为
垂直,垂足为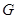 ,连结
,连结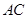 .
.
求证:(1)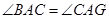 ;
;
(2)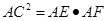 .
.
(1)利用弦切角∠BAC=∠CAG.(2)利用三角形相似。 AC2=AE·AF.
解析试题分析:(1)连结BC,∵AB是直径,
∴∠ACB=90°,∴∠ACB=∠AGC=90°.
∵GC切⊙O于C,∴∠GCA=∠ABC.
∴∠BAC=∠CAG. 5分
(2)连结CF,∵EC切⊙O于C, ∴∠ACE=∠AFC.
又∠BAC=∠CAG, ∴△ACF∽△AEC.
∴ ,∴AC2=AE·AF. 10分
,∴AC2=AE·AF. 10分
考点:本题主要考查弦切角定理,圆的性质,三角形相似。
点评:简单题,利用弦切角定理及三角形相似知识,证明角相等、确定线段长度的关系,是常见题目。

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
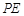 切⊙
切⊙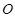 于点E,割线PBA交⊙
于点E,割线PBA交⊙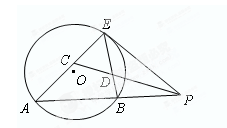
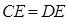 ; (Ⅱ)
; (Ⅱ)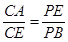 .
.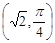 ,直线
,直线 的极坐标方程为
的极坐标方程为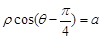 ,且点A在直线
,且点A在直线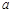 的值及直线
的值及直线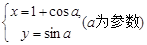 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.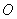 外有一点
外有一点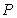 ,作圆
,作圆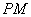 ,
,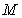 为切点,过
为切点,过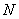 ,作割线
,作割线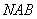 ,交圆于
,交圆于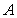 、
、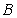 两点,连接
两点,连接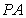 并延长,交圆
并延长,交圆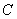 ,连续
,连续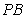 交圆
交圆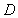 ,若
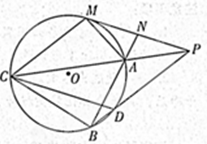
,若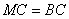 .
.
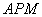 ∽△
∽△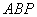 ;
;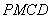 是平行四边形.
是平行四边形. 的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,
的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,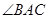 的平分线与BC和圆
的平分线与BC和圆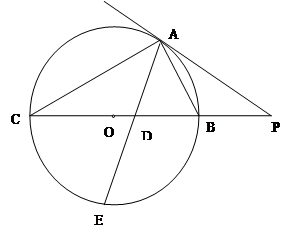
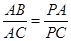 ;
;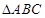 中,
中,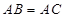 ,过点
,过点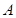 的直线与其外接圆交于点
的直线与其外接圆交于点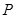 ,交
,交 延长线于点
延长线于点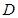 .
.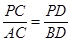 ; (2)若
; (2)若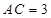 ,求
,求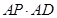
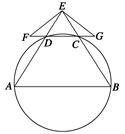
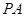 与圆
与圆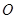 相切于点
相切于点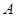 ,经过点
,经过点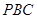 交圆
交圆 、
、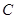 ,
,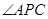 的平分线分别交
的平分线分别交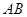 、
、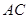 于点
于点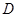 、
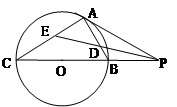
、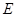 .
.
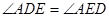 .
.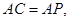 求
求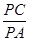 的值.
的值.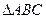 中,
中,
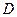 在线
在线 段
段 上,且
上,且 ,
,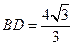
 的长;
的长; 的面积.
的面积.