题目内容
已知函数f(x)=log2(4x+1)+kx(k∈R)是偶函数.(1)求k的值;
(2)设函数
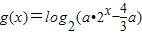 ,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.
,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.
【答案】分析:(1)由已知中函数f(x)=log2(4x+1)+kx(k∈R)是偶函数.由偶函数的定义,构造一个关于k的方程,解方程即可求出k的值;
(2)函数f(x)与g(x)的图象有且只有一个交点,即方程log2(4x+1)-x=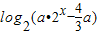 在(
在(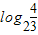 ,+∞)有且只有一解,即方程
,+∞)有且只有一解,即方程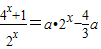 在
在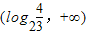 上只有一解,利用换元法,将方程转化为整式方程后,分类讨论后,即可得到a的取值范围.
上只有一解,利用换元法,将方程转化为整式方程后,分类讨论后,即可得到a的取值范围.
解答:解:(1)∵函数f(x)=log2(4x+1)+kx(k∈R)是偶函数
∴f(-x)=log2(4-x+1)-kx=f(x)=log2(4x+1)+kx恒成立
即log2(4x+1)-2x-kx=log2(4x+1)+kx恒成立
解得k=-1
(2)∵a>0
∴函数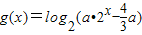 的定义域为(
的定义域为(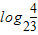 ,+∞)
,+∞)
即满足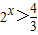
函数f(x)与g(x)的图象有且只有一个交点,
∴方程log2(4x+1)-x=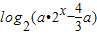 在(
在(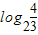 ,+∞)有且只有一解
,+∞)有且只有一解
即:方程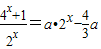 在
在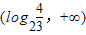 上只有一解
上只有一解
令2x=t,则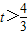 ,因而等价于关于t的方程
,因而等价于关于t的方程 (*)在
(*)在 上只有一解
上只有一解
当a=1时,解得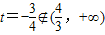 ,不合题意;
,不合题意;
当0<a<1时,记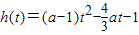 ,其图象的对称轴
,其图象的对称轴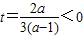
∴函数 在(0,+∞)上递减,而h(0)=-1
在(0,+∞)上递减,而h(0)=-1
∴方程(*)在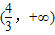 无解
无解
当a>1时,记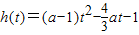 ,其图象的对称轴
,其图象的对称轴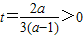
所以,只需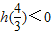 ,即
,即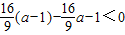 ,此恒成立
,此恒成立
∴此时a的范围为a>1
综上所述,所求a的取值范围为a>1.
点评:本题考查的知识点是函数与方程的综合运用,偶函数,其中根据偶函数的定义求出k值,进而得到函数f(x)的解析式,是解答的关键.
(2)函数f(x)与g(x)的图象有且只有一个交点,即方程log2(4x+1)-x=
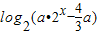 在(
在(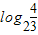 ,+∞)有且只有一解,即方程
,+∞)有且只有一解,即方程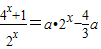 在
在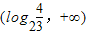 上只有一解,利用换元法,将方程转化为整式方程后,分类讨论后,即可得到a的取值范围.
上只有一解,利用换元法,将方程转化为整式方程后,分类讨论后,即可得到a的取值范围.解答:解:(1)∵函数f(x)=log2(4x+1)+kx(k∈R)是偶函数
∴f(-x)=log2(4-x+1)-kx=f(x)=log2(4x+1)+kx恒成立
即log2(4x+1)-2x-kx=log2(4x+1)+kx恒成立
解得k=-1
(2)∵a>0
∴函数
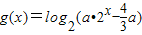 的定义域为(
的定义域为(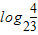 ,+∞)
,+∞)即满足
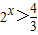
函数f(x)与g(x)的图象有且只有一个交点,
∴方程log2(4x+1)-x=
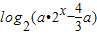 在(
在(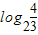 ,+∞)有且只有一解
,+∞)有且只有一解即:方程
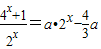 在
在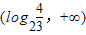 上只有一解
上只有一解令2x=t,则
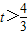 ,因而等价于关于t的方程
,因而等价于关于t的方程 (*)在
(*)在 上只有一解
上只有一解当a=1时,解得
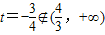 ,不合题意;
,不合题意;当0<a<1时,记
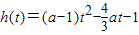 ,其图象的对称轴
,其图象的对称轴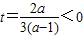
∴函数
 在(0,+∞)上递减,而h(0)=-1
在(0,+∞)上递减,而h(0)=-1∴方程(*)在
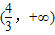 无解
无解当a>1时,记
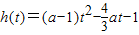 ,其图象的对称轴
,其图象的对称轴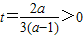
所以,只需
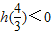 ,即
,即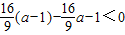 ,此恒成立
,此恒成立∴此时a的范围为a>1
综上所述,所求a的取值范围为a>1.
点评:本题考查的知识点是函数与方程的综合运用,偶函数,其中根据偶函数的定义求出k值,进而得到函数f(x)的解析式,是解答的关键.

练习册系列答案
相关题目