题目内容
5.设函数f(x)=x+ax2+blnx,曲线y=f(x)过P(1,0),且在P点处的切线斜率为2.(1)求a,b的值;
(2)当x∈[1,e]时,求f(x)的最值;
(3)证明:f(x)≤2x-2.
分析 (1)求得函数的导数,由题意可得f(1)=0,f′(1)=2,解方程可得a,b的值;
(2)求得导数,求得极值点,求出端点处的函数值,可得最值;
(3)构造函数g(x)=f(x)-(2x-2)=2-x-x2+3lnx,求出导数和单调区间,可得极值和最值,即可证得不等式.
解答 解:(1)函数f(x)=x+ax2+blnx的导数为${f}^{′}(x)=1+2ax+\frac{b}{x}$.
由已知条件得$\left\{\begin{array}{l}{f(1)=0}\\{{f}^{′}(1)=2}\end{array}\right.即\left\{\begin{array}{l}{1+a=0}\\{1+2a+b=2}\end{array}\right.$,
解得 a=-1,b=3.
(2)f(x)的定义域为(0,+∞),由(1)知f(x)=x-x2+3lnx.
令 f′(x)=0解得 $x=\frac{3}{2},x=-1$.
| x | $[1,\frac{3}{2})$ | $\frac{3}{2}$ | $(\frac{3}{2},e]$ |
| f′(x) | + | 0 | - |
| f(x) | 增 | 减 |
当x=e时,取得最小值 f(e)=e-e2+3.
(3)设g(x)=f(x)-(2x-2)=2-x-x2+3lnx,
${g}^{′}(x)=-1-2x+\frac{3}{x}=-\frac{(x-1)(2x+3)}{x}$,
当0<x<1时,g′(x)>0,当x>1时,g′(x)<0,
则g(x)在(0,1)递增,在(1,+∞)递减.
即有x=1处取得极大值,且为最大值0
故当x>0时,g(x)≤0,
即f(x)≤2x-2.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查构造函数的思想方法证明不等式,属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|(0<x≤2)}\\{-\frac{1}{2}x+2(x>2)}\end{array}\right.$,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
| A. | (1,4) | B. | (2,4) | C. | (0,8) | D. | (2,8) |
20.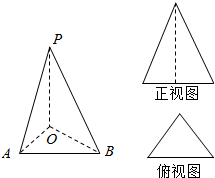 若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
 若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
17.已知{an}是等比数列,a1=8,a4=1,则公比q=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
14.某厂生产甲、乙两种产品每吨所需的煤、电和产值如表所示.
但国家每天分配给该厂的煤、电有限,每天供煤至多47吨,供电至多300千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
| 用煤(吨) | 用电(千瓦) | 产值(万元) | |
| 甲产品 | 3 | 50 | 12 |
| 乙产品 | 7 | 20 | 8 |