题目内容
已知α+β=
,则cosαcosβ-
sinαcosβ-
cosαsinβ-sinαsinβ 的值为( )
| π |
| 3 |
| 3 |
| 3 |
A.-
| B.-1 | C.1 | D.-
|
cosαcosβ-
sinαcosβ-
cosαsinβ-sinαsinβ
=(cosαcosβ-sinαsinβ )-(
sinαcosβ+
cosαsinβ)
=cos(α+β)-
sin(α+β)
=cos
-
sin
=
-
×
=-1.
故选B.
| 3 |
| 3 |
=(cosαcosβ-sinαsinβ )-(
| 3 |
| 3 |
=cos(α+β)-
| 3 |
=cos
| π |
| 3 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
=-1.
故选B.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 =______________.
=______________.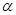 =3,则角
=3,则角 +
+ =3,则
=3,则 的值等于 .
的值等于 .