题目内容
已知α+β=
,则cosαcosβ-
sinαcosβ-
cosαsinβ-sinαsinβ 的值为( )
| π |
| 3 |
| 3 |
| 3 |
分析:把要求的式子化为(cosαcosβ-sinαsinβ )-(
sinαcosβ+
cosαsinβ),利用查两角和差的正弦、余弦公式化cos(α+β)-
sin(α+β),再把α+β=
代入运算求出结果.
| 3 |
| 3 |
| 3 |
| π |
| 3 |
解答:解:cosαcosβ-
sinαcosβ-
cosαsinβ-sinαsinβ
=(cosαcosβ-sinαsinβ )-(
sinαcosβ+
cosαsinβ)
=cos(α+β)-
sin(α+β)
=cos
-
sin
=
-
×
=-1.
故选B.
| 3 |
| 3 |
=(cosαcosβ-sinαsinβ )-(
| 3 |
| 3 |
=cos(α+β)-
| 3 |
=cos
| π |
| 3 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
=-1.
故选B.
点评:本题主要考查两角和差的正弦、余弦公式的应用,注意公式的逆用,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 =______________.
=______________.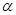 =3,则角
=3,则角 +
+ =3,则
=3,则 的值等于 .
的值等于 .