题目内容
设函数f（x）对其定义域内的任意实数
，则称函数f（x）为上凸函数．现有下列命题：①f（x）=sinx，x∈[0，π]是上凸函数；
②f（x）=lnx（x＞0）是上凸函数；
③二次函数f（x）=ax2+bx+c（a≠0）是上凸函数的充要条件是a＞0；
④f（x）是上凸函数，若A（x1，f（x1）），B（x2，f（x2））是f（x）图象上任意两点，点C在线段AB上，且
；其中，正确命题的序号是 （写出所有你认为正确命题的序号）．
【答案】分析：作图可知①②正确，③不正确，对于④，因为f（x）上凸函数，则点C在点D的下方，点C的纵坐标为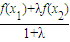
，点D的坐标为
，故
≥
．
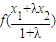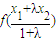解答：解；作图可知①②正确，③不正确
对于④，因为f（x）是上凸函数，则点C在点D的下方，点C的纵坐标为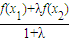
，
点D的坐标为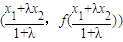
，
于是得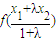
≥
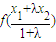，即④正确．
综上可得正确的有①②④
故答案为①②④
点评：本题考查命题真假的判断与应用，解题的关键是熟练掌握一些常见函数的性质，注意数形结合思想的灵活运用，合理地进行等价转化．
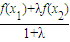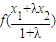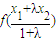，点D的坐标为，故≥．解答：解；作图可知①②正确，③不正确
对于④，因为f（x）是上凸函数，则点C在点D的下方，点C的纵坐标为
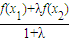，点D的坐标为
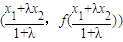，于是得
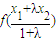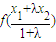≥，即④正确．综上可得正确的有①②④
故答案为①②④
点评：本题考查命题真假的判断与应用，解题的关键是熟练掌握一些常见函数的性质，注意数形结合思想的灵活运用，合理地进行等价转化．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
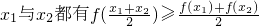，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有
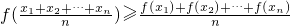（当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
；
．
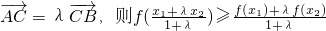，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有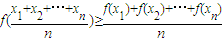
（当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
；
．