题目内容

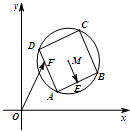（2013•丽水一模）如图，已知圆M：（x-3）2+（y-3）2=4，四边形ABCD为圆M的内接正方形，E、F分别为AB、AD的中点，当正方形ABCD绕圆心M转动，同时点F在边AD上运动时，
ME
•
OF
的最大值是
6
6
．
分析：由题意可得  
ME
•
OF
=
ME
•
OM
+
ME
•
MF
．由 ME⊥MF，可得
ME
•
MF
=0，从而
ME
•
OF
=
ME
•
OM
．
求得
ME
•
OM
=6cos＜
ME
，
OF
＞，从而求得
ME
•
OF
的最大值．
解答：解：由题意可得
OF
=
OM
+
MF
，∴
ME
•
OF
=
ME
•(
OM
+
MF
)=
ME
•
OM
+
ME
•
MF
．
∵ME⊥MF，∴
ME
•
MF
=0，∴
ME
•
OF
=
ME
•
OM
．
由题意可得，圆M的半径为2，故正方形ABCD的边长为4，故ME=
2
，
再由OM=3
2
，可得
ME
•
OM
=
2
•3
2
•cos＜
ME
，
OF
＞=6cos＜
ME
，
OF
＞，
即
ME
•
OF
=6cos＜
ME
，
OF
＞，故 
ME
•
OF
的最大值是大为6，
故答案为 6．
点评：本题主要考查两个向量的数量积的定义，两个向量的加减法的法则，以及其几何意义，余弦函数的值域，
属于中档题．
练习册系列答案
相关题目
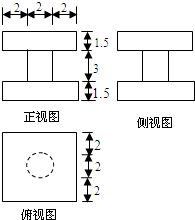（2013•丽水一模）某几何体的三视图如图所示，则该几何体的体积为
108+3π
108+3π
．
（2013•丽水一模）已知公差不为零的等差数列{an}的前10项和S10=55，且a2，a4，a8成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足bn=(-1)nan+2n，求{bn}的前n项和Tn．
（2013•丽水一模）已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1），
（Ⅰ）求抛物线的标准方程；
（Ⅱ）与圆x2+（y+1）2=1相切的直线l：y=kx+t交抛物线于不同的两点M，N，若抛物线上一点C满足
OC
=λ(
OM
+
ON
)（λ＞0），求λ的取值范围．
（2013•丽水一模）若正数a，b满足2a+b=1，则4a2+b2+
ab
的最大值为
17
16
17
16
．
（2013•丽水一模）若(x-
1
ax
)7展开式中含x的项的系数为280，则a=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网