题目内容
(2013•丽水一模)已知公差不为零的等差数列{an}的前10项和S10=55,且a2,a4,a8成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=(-1)nan+2n,求{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=(-1)nan+2n,求{bn}的前n项和Tn.
分析:(Ⅰ) 由已知条件利用等差数列的前n项和公式,等比数列的性质列出方程组求得首项和公差,即得{an}的
通项公式.
(Ⅱ)先求出数列{bn}的通项公式,分n为奇数和n为偶数两种情况,利用分组求和法分别求得{bn}的前n项
和Tn.
通项公式.
(Ⅱ)先求出数列{bn}的通项公式,分n为奇数和n为偶数两种情况,利用分组求和法分别求得{bn}的前n项
和Tn.
解答:解:(Ⅰ) 由已知得:
,化简可得
.
因为 d≠0,所以,d=a1,∴2a1+9a1=11,所以 a1=1,d=1.
所以 an=1+(n-1)=n.…(6分)
(Ⅱ)∵bn=(-1)nan+2n,∴bn=
,
∴(ⅰ) 当n为奇数时,Tn= (-1+2)+(-2+22)+(-3+23)+…+(-n+2n)
=(-1+2)+(-3+4)+(-5+6)+…+(-n)+(2+22+23+…+2n)
=
-n+
=2n+1-
-
.
(ⅱ) 当n为偶数时,Tn= (-1+2)+(-2+22)+(-3+23)+…+(-n+2n)
=(-1+2)+(-3+4)+(-5+6)+…+(-n+1+n)+(2+22+23+…+2n)
=2n+1 +
-2.
所以,Tn=
.…(14分)
|
|
因为 d≠0,所以,d=a1,∴2a1+9a1=11,所以 a1=1,d=1.
所以 an=1+(n-1)=n.…(6分)
(Ⅱ)∵bn=(-1)nan+2n,∴bn=
|
∴(ⅰ) 当n为奇数时,Tn= (-1+2)+(-2+22)+(-3+23)+…+(-n+2n)
=(-1+2)+(-3+4)+(-5+6)+…+(-n)+(2+22+23+…+2n)
=
| n-1 |
| 2 |
| 2(1-2n) |
| 1-2 |
| n |
| 2 |
| 5 |
| 2 |
(ⅱ) 当n为偶数时,Tn= (-1+2)+(-2+22)+(-3+23)+…+(-n+2n)
=(-1+2)+(-3+4)+(-5+6)+…+(-n+1+n)+(2+22+23+…+2n)
=2n+1 +
| n |
| 2 |
所以,Tn=
|
点评:本题主要考查等差数列的前n项和公式,等比数列的性质,数列求和,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
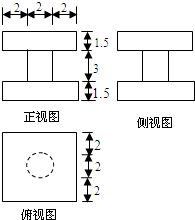 (2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为
(2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为 (2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),
(2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),