题目内容
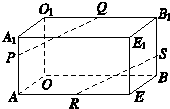
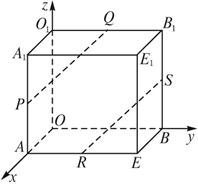
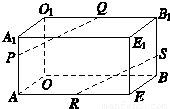
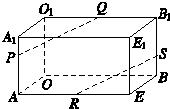如图，在长方体OAEB-O1A1E1B1中，OA=3，OB=4，OO1=2，点P在棱AA1上，且AP=2PA1，点S在棱BB1上，且SB1=2BS，点Q、R分别是O1B1、AE的中点，求证：PQ∥RS．分析：根据条件中的长方体建立空间直角坐标系，写出点的坐标，再求得向量
，
的坐标，利用向量平行的条件得出
∥
，从而得出PQ∥RS．
| PQ |
| RS |
| PQ |
| RS |
解答：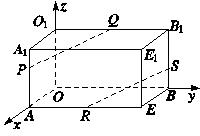
证明：如图，建立空间直角坐标系，则A（3，0，0），B（0，4，0），O1（0，0，2），
A1（3，0，2），B1（0，4，2），E（3，4，0），
∵AP=2PA1，∴
=2
=
，
即
=
（0，0，2）=（0，0，
），∴P（3，0，
）
同理可得，Q（0，2，2），R（3，2，0），S（0，4，
），
∴
=（-3，2，
）=
，
∴
∥
，
∵R∉PQ，
∴PQ∥RS
证明：如图，建立空间直角坐标系，则A（3，0，0），B（0，4，0），O1（0，0，2），A1（3，0，2），B1（0，4，2），E（3，4，0），
∵AP=2PA1，∴
| AP |
| PA1 |
| 2 |
| 3 |
| AA1 |
即
| AP |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
同理可得，Q（0，2，2），R（3，2，0），S（0，4，
| 2 |
| 3 |
∴
| PQ |
| 2 |
| 3 |
| RS |
∴
| PQ |
| RS |
∵R∉PQ，
∴PQ∥RS
点评：本题考查向量语言表述线线的垂直、平行关系．根据空间直角坐标系写出点的坐标的问题，这种问题是为解决空间向量与立体几何做准备，是一个基础题，注意数字运算不要出错．
练习册系列答案
阅读快车系列答案
相关题目
