题目内容
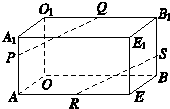
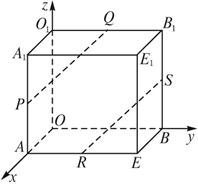
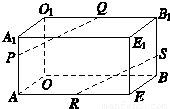
如图,在长方体OAEB-O1A1E1B1中,|OA|=3,|OB|=4,|OO1|=2,点P在棱AA1上,且|AP|=2|PA1|,点S在棱BB1上,且|SB1|=2|BS|,点Q、R分别是棱O1B1、AE的中点.

求证:PQ∥RS.
答案:
解析:
提示:
解析:
|
证明:如图,建立空间直角坐标系,则A(3,0,0),B(0,4,0),O1(0,0,2),A1(3,0,2),B1(0,4,2). 因为|PA|=2|PA1|,|SB1|=2|BS|,Q、R分别是棱O1B1、AE的中点, 所以P(3,0, 于是 ∴ ∴ |
提示:
|
利用向量证明PQ平行于RS,只需建立适当的坐标系,表示出 |

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
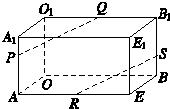 如图,在长方体OAEB-O1A1E1B1中,OA=3,OB=4,OO1=2,点P在棱AA1上,且AP=2PA1,点S在棱BB1上,且SB1=2BS,点Q、R分别是O1B1、AE的中点,求证:PQ∥RS.
如图,在长方体OAEB-O1A1E1B1中,OA=3,OB=4,OO1=2,点P在棱AA1上,且AP=2PA1,点S在棱BB1上,且SB1=2BS,点Q、R分别是O1B1、AE的中点,求证:PQ∥RS.