题目内容
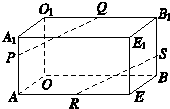
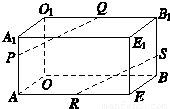
如图,在长方体OAEB—O1A1E1B1中,|OA|=3,|OB|=4,|OO1|=2,点P在棱AA1上,且|AP|=2|PA1|,点S在棱BB1上,且|SB1|=2|BS|,点Q、R分别是棱O1B1、AE的中点.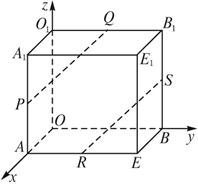
求证:PQ∥RS.
证明:如图,建立空间直角坐标系,则A(3,0,0),B(0,4,0),O1(0,0,2),A1(3,0,2),B1(0,4,2).
由定比分点公式,得P(3,0,![]() ),Q(0,2,2),R(3,2,0),S(0,4,
),Q(0,2,2),R(3,2,0),S(0,4,![]() ),
),
于是![]() ,
,
∴![]() .∵R
.∵R![]() PQ,∴PQ∥RS.
PQ,∴PQ∥RS.
启示:利用向量坐标运算证明线线平行时,(1)需证明两向量共线;(2)证明其中一个向量所在直线上一点不在另一个向量所在的直线上.建立恰当的空间直角坐标系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
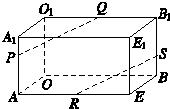 如图,在长方体OAEB-O1A1E1B1中,OA=3,OB=4,OO1=2,点P在棱AA1上,且AP=2PA1,点S在棱BB1上,且SB1=2BS,点Q、R分别是O1B1、AE的中点,求证:PQ∥RS.
如图,在长方体OAEB-O1A1E1B1中,OA=3,OB=4,OO1=2,点P在棱AA1上,且AP=2PA1,点S在棱BB1上,且SB1=2BS,点Q、R分别是O1B1、AE的中点,求证:PQ∥RS.