题目内容
一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是| 2 |
| 5 |
| 7 |
| 9 |
(Ⅰ)若袋中共有10个球,从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的数学期望Eξ.
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于
| 7 |
| 10 |
分析:(I)首先根据从袋中任意摸出2个球,至少得到1个白球的概率是
,列出关系式,得到白球的个数,从袋中任意摸出3个球,白球的个数为ξ,根据题意得到变量可能的取值,结合对应的事件,写出分布列和期望.
(II)设出两种球的个数,根据从袋中任意摸出2个球,至少得到1个黑球的概率不大于
,得到两个未知数之间的关系,得到白球的个数比黑球多,白球个数多于
n,红球的个数少于
,得到袋中红球个数最少.
| 7 |
| 9 |
(II)设出两种球的个数,根据从袋中任意摸出2个球,至少得到1个黑球的概率不大于
| 7 |
| 10 |
| 2 |
| 5 |
| n |
| 5 |
解答:解:(Ⅰ)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,
设袋中白球的个数为x,
则P(A)=1-
=
,
得到x=5.
故白球有5个.
随机变量ξ的取值为0,1,2,3,
∴分布列是
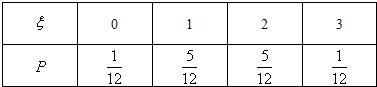
∴ξ的数学期望Eξ=
×0+
×1+
×2+
×3=
.
(Ⅱ)证明:设袋中有n个球,其中y个黑球,由题意得y=
n,
∴2y<n,2y≤n-1,
故
≤
.
记“从袋中任意摸出两个球,至少有1个黑球”为事件B,
则P(B)=
+
×
≤
+
×
=
.
∴白球的个数比黑球多,白球个数多于
n,红球的个数少于
.
故袋中红球个数最少.
设袋中白球的个数为x,
则P(A)=1-
| ||
|
| 7 |
| 9 |
得到x=5.
故白球有5个.
随机变量ξ的取值为0,1,2,3,
∴分布列是

∴ξ的数学期望Eξ=
| 1 |
| 12 |
| 5 |
| 12 |
| 5 |
| 12 |
| 1 |
| 12 |
| 3 |
| 2 |
(Ⅱ)证明:设袋中有n个球,其中y个黑球,由题意得y=
| 2 |
| 5 |
∴2y<n,2y≤n-1,
故
| y |
| n-1 |
| 1 |
| 2 |
记“从袋中任意摸出两个球,至少有1个黑球”为事件B,
则P(B)=
| 2 |
| 5 |
| 3 |
| 5 |
| y |
| n-1 |
| 2 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 7 |
| 10 |
∴白球的个数比黑球多,白球个数多于
| 2 |
| 5 |
| n |
| 5 |
故袋中红球个数最少.
点评:本题主要考查排列组合、对立事件、相互独立事件的概率和随机变量分布列和数学期望等概念,同时考查学生的逻辑思维能力和分析问题以及解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
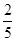 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是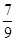 。
。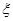 ,求随机变量
,求随机变量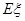 。
。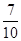 。并指出袋中哪种颜色的球个数最少。
。并指出袋中哪种颜色的球个数最少。