题目内容
一个袋中有若干个大小相同的小球,分别编有一个1号,两个2号,m个3号和n个4号.已知从袋中任意摸出2个球,至少得到1个4号球的概率是| 2 | 3 |
(i)求4号球的个数;
(ii)从袋中任意摸出2个球,记得到小球的编号数之和为ξ,求随机变量ξ的分布列和数学期望Eξ.
分析:(i)由题意可得:从袋中10个球中任意摸出2个球,共有的取法有C102,至少有1个4号球的取法有Cn2+Cn1C10-n1,结合题意即可求出答案.
(ii)由题意可得:随机变量ξ可能取的值为3,4,5,6,7,8,根据题意分别求出其发生的概率,进而求出离散型随机变量的分布列与数学期望.
(ii)由题意可得:随机变量ξ可能取的值为3,4,5,6,7,8,根据题意分别求出其发生的概率,进而求出离散型随机变量的分布列与数学期望.
解答:解:(i)由题意可得:从袋中10个球中任意摸出2个球,共有的取法有C102,
至少有1个4号球的取法有Cn2+Cn1C10-n1,
因为至少得到1个4号球的概率是
,即
,
所以n=4.
(ii)由题意可得:随机变量ξ可能取的值为3,4,5,6,7,8,
所以由题意可得:P(ξ=3)=
,p(ξ=4)=
,p(ξ=5)=
=
,p(ξ=6)=
,p(ξ=7)=
=
,p(ξ=8)=
=
,
所以ξ的分布列为:
所以ξ的数学期望为:Eξ=6.
至少有1个4号球的取法有Cn2+Cn1C10-n1,
因为至少得到1个4号球的概率是
| 2 |
| 3 |
|
所以n=4.
(ii)由题意可得:随机变量ξ可能取的值为3,4,5,6,7,8,
所以由题意可得:P(ξ=3)=
| 2 |
| 45 |
| 4 |
| 45 |
| 10 |
| 45 |
| 2 |
| 9 |
| 11 |
| 45 |
| 12 |
| 45 |
| 4 |
| 15 |
| 6 |
| 45 |
| 2 |
| 15 |
所以ξ的分布列为:
| ξ | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||||||
| p |
|
|
|
|
|
|
点评:本题主要考查离散型随机变量的分布列与数学期望.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
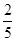 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是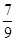 。
。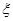 ,求随机变量
,求随机变量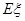 。
。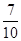 。并指出袋中哪种颜色的球个数最少。
。并指出袋中哪种颜色的球个数最少。