题目内容
一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球,得到黑球的概率是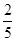 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是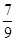 。
。
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为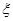 ,求随机变量
,求随机变量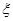 的数学期望
的数学期望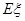 。
。
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于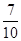 。并指出袋中哪种颜色的球个数最少。
。并指出袋中哪种颜色的球个数最少。
【答案】
解:(Ⅰ)当 时,
时,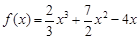 ,则
,则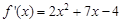 =
=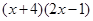
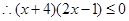 ,
,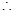
 的单调递减区间是
的单调递减区间是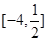
(II)∵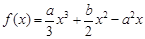 ,∴
,∴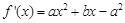 .
.
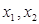 是函数
是函数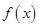 的两个不同的极值点,则
的两个不同的极值点,则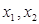 是方程
是方程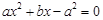 的两个不同的实数根,
的两个不同的实数根,
即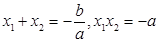 ,且
,且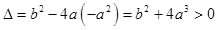
∵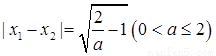 ,即
,即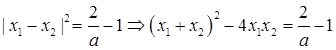
∴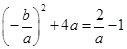 ,即
,即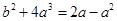 ,则
,则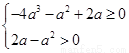
即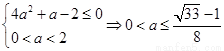 ,又
,又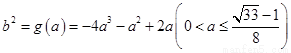
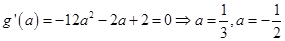 (舍)
(舍)
当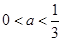 时,
时,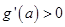 ,
,
 是增函数;当
是增函数;当 时,
时, ,
,
 是减函数;
是减函数;
 取到最大值
取到最大值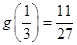 ,
,
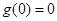 ,又
,又 是
是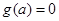 的根,
的根,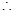
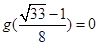
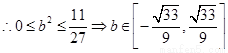 .
.
【解析】略

练习册系列答案
相关题目