题目内容
已知x=1是函数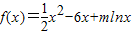 的一个极值点.
的一个极值点.(Ⅰ)求m;
(Ⅱ)若直线y=n与函数y=f(x)的图象有3个交点,求n的取值范围;
(Ⅲ)设g(x)=(-5-a)lnx+
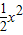 +(6-b)x+2(a>0),G(x)=f(x)+g(x),若G(x)=0有两个不同零点x1,x2,且
+(6-b)x+2(a>0),G(x)=f(x)+g(x),若G(x)=0有两个不同零点x1,x2,且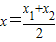 ,试探究G′(x)值的符号.
,试探究G′(x)值的符号.
【答案】分析:(Ⅰ)求导数f′(x),令f′(1)=0即可求得m值;
(Ⅱ)利用导数可求得函数f(x)的单调区间,由单调区间可得函数极大值、极小值,结合图象n大于极小值小于极小值,从而得到n的范围;
(Ⅲ)化简G(x),则G(x1)=0,G(x2)=0,两式相减并变形可得 ,于是G′(x)可用x1,x2表示,构造关于t=
,于是G′(x)可用x1,x2表示,构造关于t=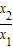 的函数,按0<x1<x2,0<x2<x1两种情况进行讨论可判断G′(x)的符号;
的函数,按0<x1<x2,0<x2<x1两种情况进行讨论可判断G′(x)的符号;
解答:解:(Ⅰ)因为f′(x)x-6+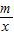 ,
,
所以f′(1)=1-6+m=0,解得m=5;
(Ⅱ)由(Ⅰ)知f(x)=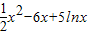 (x>0),
(x>0),
所以f′(x)=x-6+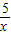 =
=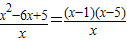 ,
,
当x∈(1,5)时,f′(x)<0,f(x)单调递减;
当x∈(5,+∞)或x∈(0,1)时,f′(x)>0,f(x)单调递增.
所以f(x)的极大值为f(1)=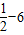 =-
=-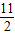 ,
,
极小值为f(5)=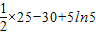 =-
=-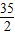 +5ln5,
+5ln5,
又x→0时,f(x)→-∞,x→+∞时,f(x)→+∞,
结合图象可知:当且仅当f(5)<n<f(1)时,直线y=n与函数y=f(x)的图象有3个交点,
∴-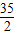 +5ln5<n<-
+5ln5<n<-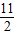 ;
;
(III)G′(x)的符号为正.证明如下:
因为G(x)=f(x)+g(x)=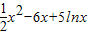 +(-5-a)lnx+
+(-5-a)lnx+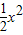 +(6-b)x+2=x2+2-alnx-bx有两个零点x1,x2,
+(6-b)x+2=x2+2-alnx-bx有两个零点x1,x2,
所以有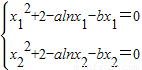 ,
,
两式相减得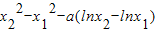 -b(x2-x1)=0,即
-b(x2-x1)=0,即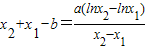 ,
,
于是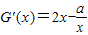 -b=
-b=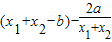
= -
-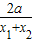 =
=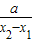 [ln
[ln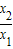 -
-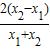 ]=
]=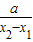 [ln
[ln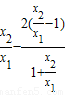 ],
],
①,令 =t,则t>1,且G′(x)=
=t,则t>1,且G′(x)=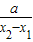 (lnt-
(lnt-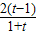 ).
).
设u(t)=lnt-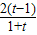 (t>1),
(t>1),
则u′(t)=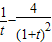 =
=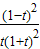 >0,
>0,
则u(t)=lnt-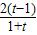 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
而u(1)=0,所以u(t)>0,即lnt-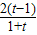 >0.
>0.
又因为a>0,x2-x1>0,所以G′(x)>0.
②当0<x2<x1时,同理可得:G′(x)>0.
综上所述:G′(x)的符号为正.
点评:本题考查利用导数研究函数的极值、函数的零点等知识,考查分类讨论思想、数形结合思想及函数与方程思想,考查学生综合运用所学知识分析解决问题的能力,综合性强,难度较大.
(Ⅱ)利用导数可求得函数f(x)的单调区间,由单调区间可得函数极大值、极小值,结合图象n大于极小值小于极小值,从而得到n的范围;
(Ⅲ)化简G(x),则G(x1)=0,G(x2)=0,两式相减并变形可得
 ,于是G′(x)可用x1,x2表示,构造关于t=
,于是G′(x)可用x1,x2表示,构造关于t=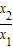 的函数,按0<x1<x2,0<x2<x1两种情况进行讨论可判断G′(x)的符号;
的函数,按0<x1<x2,0<x2<x1两种情况进行讨论可判断G′(x)的符号;解答:解:(Ⅰ)因为f′(x)x-6+
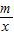 ,
,所以f′(1)=1-6+m=0,解得m=5;
(Ⅱ)由(Ⅰ)知f(x)=
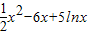 (x>0),
(x>0),所以f′(x)=x-6+
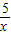 =
=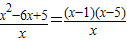 ,
,当x∈(1,5)时,f′(x)<0,f(x)单调递减;
当x∈(5,+∞)或x∈(0,1)时,f′(x)>0,f(x)单调递增.
所以f(x)的极大值为f(1)=
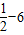 =-
=-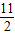 ,
,极小值为f(5)=
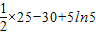 =-
=-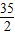 +5ln5,
+5ln5,又x→0时,f(x)→-∞,x→+∞时,f(x)→+∞,
结合图象可知:当且仅当f(5)<n<f(1)时,直线y=n与函数y=f(x)的图象有3个交点,
∴-
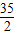 +5ln5<n<-
+5ln5<n<-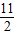 ;
;(III)G′(x)的符号为正.证明如下:
因为G(x)=f(x)+g(x)=
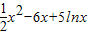 +(-5-a)lnx+
+(-5-a)lnx+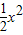 +(6-b)x+2=x2+2-alnx-bx有两个零点x1,x2,
+(6-b)x+2=x2+2-alnx-bx有两个零点x1,x2,所以有
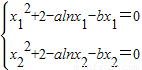 ,
,两式相减得
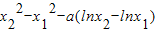 -b(x2-x1)=0,即
-b(x2-x1)=0,即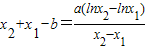 ,
,于是
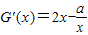 -b=
-b=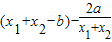
=
 -
-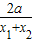 =
=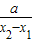 [ln
[ln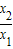 -
-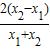 ]=
]=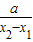 [ln
[ln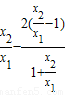 ],
],①,令
 =t,则t>1,且G′(x)=
=t,则t>1,且G′(x)=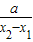 (lnt-
(lnt-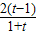 ).
).设u(t)=lnt-
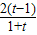 (t>1),
(t>1),则u′(t)=
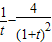 =
=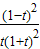 >0,
>0,则u(t)=lnt-
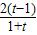 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.而u(1)=0,所以u(t)>0,即lnt-
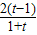 >0.
>0.又因为a>0,x2-x1>0,所以G′(x)>0.
②当0<x2<x1时,同理可得:G′(x)>0.
综上所述:G′(x)的符号为正.
点评:本题考查利用导数研究函数的极值、函数的零点等知识,考查分类讨论思想、数形结合思想及函数与方程思想,考查学生综合运用所学知识分析解决问题的能力,综合性强,难度较大.

练习册系列答案
相关题目