题目内容
己知函数f(x)=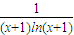 .
.(1)求函数f(x)的定义域;
(2)求函数f(x)的增区间;
(3)是否存在实数m,使不等式
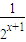 >(x+1)m在-1<x<0时恒成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
>(x+1)m在-1<x<0时恒成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
【答案】分析:(1)先根据函数解析式得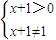 解之即得函数f(x)的定义域;
解之即得函数f(x)的定义域;
(2)在(1)中确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0,解得的区间就是单调增区间.
(3)根据已知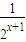 >(x+1)m在-1<x<0时恒成立等价于
>(x+1)m在-1<x<0时恒成立等价于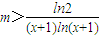 恒成立,构造新的函数h(x)=
恒成立,构造新的函数h(x)= 本题所要求的m的取值范围,只需m>h(x)最大值即可.
本题所要求的m的取值范围,只需m>h(x)最大值即可.
解答:解:(1)根据函数解析式得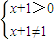 ,
,
解得x>-1且x≠0.∴函数f(x)的定义域是x|x∈R,x>-1且x≠0.(3分)
(2)∵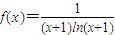 ,∴
,∴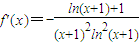 (5分)
(5分)
由f'(x)>0得ln(x+1)+1<0.∴-1<x<e-1-1.∴函数f(x)的增区间为(-1,e-1-1).(8分)
(3)∵e-1-1<x<0,∴e-1<x+1<1.∴-1<ln(x+1)<0.∴ln(x+1)+1>0∴当e-1-1<x<0时,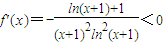 .∴在区间(-1,0)上,
.∴在区间(-1,0)上,
当x=e-1-1时,f(x)取得最大值.∴[f(x)]最大=f(e-1-1)=-e.(10分)
∵ 在-1<x<0时恒成立.∴
在-1<x<0时恒成立.∴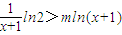 在-1<x<0时恒成立.
在-1<x<0时恒成立.
∴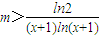 在-1<x<0时恒成立.∵
在-1<x<0时恒成立.∵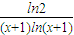 在-1<x<0时的最大值等于-eln2.
在-1<x<0时的最大值等于-eln2.
∴m>-eln2.∴当m>-eln2时,不等式 在-1<x<0,时恒成立.(14分)
在-1<x<0,时恒成立.(14分)
点评:本小题主要考查函数与导数等知识,考查分类讨论,化归与转化的数学思想方法,以及推理论证能力和运算求解能力.利用导数判断函数的单调性的步骤是:(1)确定函数的定义域;(2)求导数fˊ(x);(3)在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定函数的单调区间.若在函数式中含字母系数,往往要分类讨论.
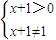 解之即得函数f(x)的定义域;
解之即得函数f(x)的定义域;(2)在(1)中确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0,解得的区间就是单调增区间.
(3)根据已知
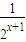 >(x+1)m在-1<x<0时恒成立等价于
>(x+1)m在-1<x<0时恒成立等价于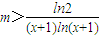 恒成立,构造新的函数h(x)=
恒成立,构造新的函数h(x)= 本题所要求的m的取值范围,只需m>h(x)最大值即可.
本题所要求的m的取值范围,只需m>h(x)最大值即可.解答:解:(1)根据函数解析式得
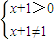 ,
,解得x>-1且x≠0.∴函数f(x)的定义域是x|x∈R,x>-1且x≠0.(3分)
(2)∵
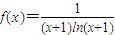 ,∴
,∴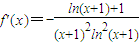 (5分)
(5分)由f'(x)>0得ln(x+1)+1<0.∴-1<x<e-1-1.∴函数f(x)的增区间为(-1,e-1-1).(8分)
(3)∵e-1-1<x<0,∴e-1<x+1<1.∴-1<ln(x+1)<0.∴ln(x+1)+1>0∴当e-1-1<x<0时,
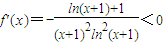 .∴在区间(-1,0)上,
.∴在区间(-1,0)上,当x=e-1-1时,f(x)取得最大值.∴[f(x)]最大=f(e-1-1)=-e.(10分)
∵
 在-1<x<0时恒成立.∴
在-1<x<0时恒成立.∴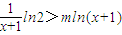 在-1<x<0时恒成立.
在-1<x<0时恒成立.∴
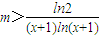 在-1<x<0时恒成立.∵
在-1<x<0时恒成立.∵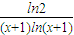 在-1<x<0时的最大值等于-eln2.
在-1<x<0时的最大值等于-eln2.∴m>-eln2.∴当m>-eln2时,不等式
 在-1<x<0,时恒成立.(14分)
在-1<x<0,时恒成立.(14分)点评:本小题主要考查函数与导数等知识,考查分类讨论,化归与转化的数学思想方法,以及推理论证能力和运算求解能力.利用导数判断函数的单调性的步骤是:(1)确定函数的定义域;(2)求导数fˊ(x);(3)在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定函数的单调区间.若在函数式中含字母系数,往往要分类讨论.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
己知函数f(x)=3cos(2x-
)(x∈R),则下列结论错误的是( )
| π |
| 3 |
A、函数f(x)的图象的一条对称轴为x=
| ||||
B、点(-
| ||||
C、函数f(x)在区间(
| ||||
D、函数f(x)的图象可以由函数g(x)=3cos2x图象向右平移
|