题目内容
(本小题满分12分)
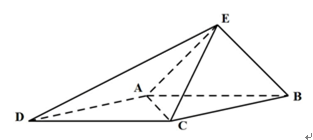
如图1,在Rt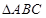 中,
中, ,
, .D、E分别是
.D、E分别是 上的点,且
上的点,且 ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.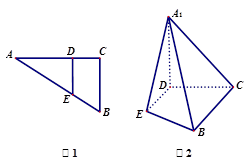
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)若 ,求
,求 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当 点在何处时,
点在何处时, 的长度最小,并求出最小值.
的长度最小,并求出最小值.
(Ⅰ)证明:在△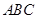 中,
中,
结合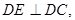 推出
推出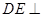 平面
平面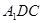 .
.
再根据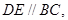 得到
得到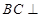 平面
平面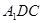 ,平面
,平面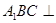 平面
平面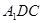 。
。
(Ⅱ)直线BE与平面 所成角的余弦值为
所成角的余弦值为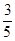 .
.
(Ⅲ)当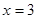 时
时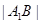 最大为
最大为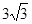 。
。
解析试题分析:(Ⅰ)证明:在△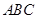 中,
中,
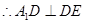 .又
.又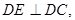
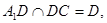
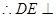 平面
平面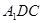 .
.
又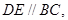
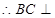 平面
平面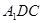 ,又
,又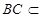 平面
平面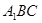 ,故平面
,故平面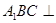 平面
平面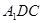 ……(4分)
……(4分)
(Ⅱ)由(1)知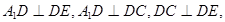 故以D为原点,
故以D为原点, 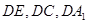 分别为x,y,z轴建立直角坐标系. 因为CD="2," 则
分别为x,y,z轴建立直角坐标系. 因为CD="2," 则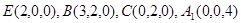 …(5分)
…(5分) ,设平面
,设平面 的一个法向量为
的一个法向量为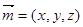
则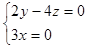 取法向量
取法向量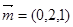 ,则直线BE与平面
,则直线BE与平面 所成角
所成角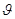 ,
,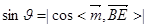
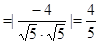 ………………(8分)
………………(8分)
故直线BE与平面 所成角的余弦值为
所成角的余弦值为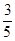 . …………………(9分)
. …………………(9分)
(Ⅲ)设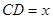 ,则
,则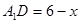 ,则
,则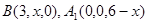 ,
,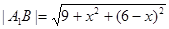
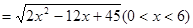 ,则当
,则当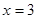 时
时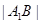 最大为
最大为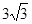 .…(12分)
.…(12分)
考点:本题主要考查立体几何中的垂直关系,距离及角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用向量则能简化证明过程。本题(3),得到距离表达式后,应用了二次函数在指定区间的最值求法,达到解题目的。

练习册系列答案
相关题目
 中,
中, ,
, ,
, ,
, ,
, , 点
, 点 ,
, 分别在棱
分别在棱 上,且
上,且 ,
,
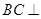 平面PAC
平面PAC 的中点时,求
的中点时,求 与平面
与平面 所成的角的正弦值;
所成的角的正弦值; 为直二面角?并说明理由.
为直二面角?并说明理由. 中,点
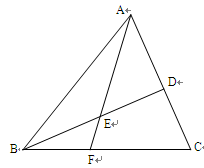
中,点 是
是 的中点,点
的中点,点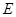 是
是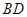 的中点,
的中点,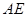 的延长线交
的延长线交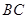 与点
与点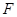 。
。
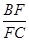 的值;
的值;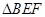 的面积为
的面积为 ,四边形
,四边形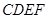 的面积为
的面积为 ,求
,求 的值。
的值。 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, ,
, ,
,  是
是 的中点.
的中点.
 平面
平面 ;
; ;
; 中,
中,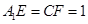 .
.
 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.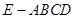 的底面为菱形,且
的底面为菱形,且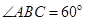 ,
,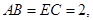
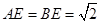 ,
,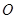 为
为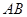 的中点.
的中点.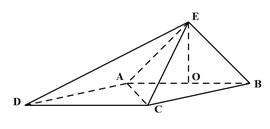
 平面
平面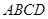 ;
;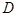 到面
到面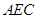 的距离.
的距离.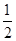 PD.
PD.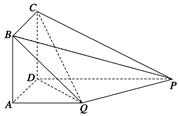
 中,
中, ,
, .
.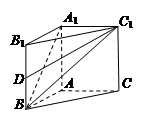
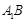 与
与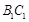 所成的角为
所成的角为 ,求棱柱的高;
,求棱柱的高;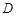 是
是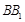 的中点,
的中点,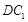 与平面
与平面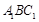 所成的角为
所成的角为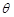 ,当棱柱的高变化时,求
,当棱柱的高变化时,求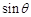 的最大值.
的最大值.