题目内容
如果二次函数y=x2-（a-1）x+5在（0，1）是增函数，那么f（2）的取值范围是 ．
【答案】分析：求出二次函数f（x）=x2-（a-1）x+5的对称轴，根据题意求出a的范围，再利用不等式的性质即可求出f（2）的取值范围．
解答：解：二次函数f（x）=x2-（a-1）x+5的对称轴为x=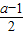
，开口向上，
又二次函数f（x）在区间（0，1）上为增函数，
则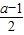
≤0，解得a≤1，
f（2）=4-2（a-1）+5=9-2（a-1）=11-2a，11-2a≥11-2=9，
故f（2）的取值范围是[9，+∞）．
故答案为：[9，+∞）．
点评：此题主要考查二次函数的单调性、函数值的求解及不等式的性质，属中档题．
解答：解：二次函数f（x）=x2-（a-1）x+5的对称轴为x=
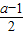，开口向上，又二次函数f（x）在区间（0，1）上为增函数，
则
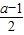≤0，解得a≤1，f（2）=4-2（a-1）+5=9-2（a-1）=11-2a，11-2a≥11-2=9，
故f（2）的取值范围是[9，+∞）．
故答案为：[9，+∞）．
点评：此题主要考查二次函数的单调性、函数值的求解及不等式的性质，属中档题．
练习册系列答案
阅读快车系列答案
相关题目