题目内容
 (选修4-1几何证明选讲)
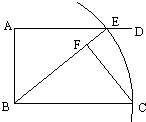
(选修4-1几何证明选讲)如图,AD∥BC,∠A=90°,以点B为圆心,BC长为半径画弧,交射线AD于点E,连接BE,过点C作CF⊥BE,垂足为F
求证:AB=FC.
分析:由题意得BC=BE,再根据矩形的性质得∠A=90°,AE∥BC,则∠AEB=∠FBC,而CF丄BE,则∠BFC=90°,根据直角三角形全等的判定易得到Rt△ABE≌Rt△CFB,利用三角形全等的性质即可得到AB=FC.
解答:证明:∵以点B为圆心、BC长为半径画弧,交AD边于点E,
∴BC=BE,
∵四边形ABCD为矩形,
∴∠A=90°,AE∥BC,
∴∠AEB=∠FBC,
而CF丄BE,∴∠BFC=90°,
在Rt△ABE和Rt△FCB中,
BE=BC,∠AEB=∠FBC,
∴Rt△ABE≌Rt△FCB,
∴AB=FC.
∴BC=BE,
∵四边形ABCD为矩形,
∴∠A=90°,AE∥BC,
∴∠AEB=∠FBC,
而CF丄BE,∴∠BFC=90°,
在Rt△ABE和Rt△FCB中,
BE=BC,∠AEB=∠FBC,
∴Rt△ABE≌Rt△FCB,
∴AB=FC.
点评:本题考查了全等三角形的判定与性质:有一组锐角对应相等,一组对应边相等的两个直角三角形全等;全等三角形的对应边相等.属于基础题.

练习册系列答案
相关题目
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线 已知△ABC中AB=AC,D为△ABC外接圆劣弧,
已知△ABC中AB=AC,D为△ABC外接圆劣弧,
 (2013•辽宁)(选修4-1几何证明选讲)
(2013•辽宁)(选修4-1几何证明选讲) (2011•南京模拟)A.选修4-1几何证明选讲
(2011•南京模拟)A.选修4-1几何证明选讲