题目内容
(2012•石家庄一模)选修4-1几何证明选讲
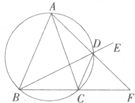 已知△ABC中AB=AC,D为△ABC外接圆劣弧,
已知△ABC中AB=AC,D为△ABC外接圆劣弧,
上的点(不与点A、C重合),延长BD至E,延长AD交BC的延长线于F.
(I)求证.∠CDF=∠EDF
(II)求证:AB•AC•DF=AD•FC•FB.
 已知△ABC中AB=AC,D为△ABC外接圆劣弧,
已知△ABC中AB=AC,D为△ABC外接圆劣弧, | AC |
(I)求证.∠CDF=∠EDF
(II)求证:AB•AC•DF=AD•FC•FB.
分析:(I)根据A,B,C,D 四点共圆,可得∠ABC=∠CDF,AB=AC可得∠ABC=∠ACB,从而得解.
(II)证明△BAD∽△FAB,可得AB2=AD•AF,因为AB=AC,所以AB•AC=AD•AF,再根据割线定理即可得到结论.
(II)证明△BAD∽△FAB,可得AB2=AD•AF,因为AB=AC,所以AB•AC=AD•AF,再根据割线定理即可得到结论.
解答:证明:(I)∵A,B,C,D 四点共圆,∴∠ABC=∠CDF
又AB=AC∴∠ABC=∠ACB,
且∠ADB=∠ACB,∴∠ADB=∠CDF,7分
对顶角∠EDF=∠ADB,故∠EDF=∠CDF;
(II)由(I)得∠ADB=∠ABF
∵∠BAD=∠FAB
∴△BAD∽△FAB
∴
=
∴AB2=AD•AF
∵AB=AC
∴AB•AC=AD•AF
∴AB•AC•DF=AD•AF•DF
根据割线定理DF•AF=FC•FB
∴AB•AC•DF=AD•FC•FB
又AB=AC∴∠ABC=∠ACB,
且∠ADB=∠ACB,∴∠ADB=∠CDF,7分
对顶角∠EDF=∠ADB,故∠EDF=∠CDF;
(II)由(I)得∠ADB=∠ABF
∵∠BAD=∠FAB
∴△BAD∽△FAB
∴
| AB |
| AF |
| AD |
| AB |
∴AB2=AD•AF
∵AB=AC
∴AB•AC=AD•AF
∴AB•AC•DF=AD•AF•DF
根据割线定理DF•AF=FC•FB
∴AB•AC•DF=AD•FC•FB
点评:本题以圆为载体,考查圆的内接四边形的性质,考查等腰三角形的性质,考查三角形的相似,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 (2012•石家庄一模)函数f(x)=Asin(ωx+φ)(A,ω,φ)为常数,A>0,ω>0的部分图象如图所示,则f(0)的值为( )
(2012•石家庄一模)函数f(x)=Asin(ωx+φ)(A,ω,φ)为常数,A>0,ω>0的部分图象如图所示,则f(0)的值为( ) (2012•石家庄一模)函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则f(0)的值是( )
(2012•石家庄一模)函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则f(0)的值是( )