题目内容
 (2011•南京模拟)A.选修4-1几何证明选讲
(2011•南京模拟)A.选修4-1几何证明选讲如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC交于点D.
求证:ED2=EB•EC.
B.矩阵与变换
已知矩阵A=
|
|
C.选修4-4 参数方程与极坐标
若两条曲线的极坐标方程分别为ρ=1与ρ=2cos(θ+
| π |
| 3 |
D.选修4-5 不等式证明选讲设a,b,c为正实数,求证:a3+b3+c3+
| 1 |
| abc |
| 3 |
分析:A、由切割线定理可得 EA2=EB•EC,证明∠EAD=∠EDA,△EAD为等腰三角形,得EA=ED,从而ED2=EB•EC 成立.
B、设 X=
,求出AX,再由AX=B,解方程组求得a、b、c、d的值,接口求得X.
C、把曲线的极坐标方程化为直角坐标方程,她们都表示圆,求出它们的圆心和半径,由弦长公式求出弦长AB的值.
D、利用基本不等式证明要证的不等式,注意检验等号成立的条件.
B、设 X=
|
C、把曲线的极坐标方程化为直角坐标方程,她们都表示圆,求出它们的圆心和半径,由弦长公式求出弦长AB的值.
D、利用基本不等式证明要证的不等式,注意检验等号成立的条件.
解答:解:A 由切割线定理可得 EA2=EB•EC.
再由同弧所对的圆周角等于该弧所对的弦切角可得∠ABC=∠CAE.
又AD是∠BAC的平分线,故有∠BAD=∠CAD.
再由∠EAD=∠EAC+∠CAD,∠EDA=∠BAD+∠ABC 可得∠EAD=∠EDA.
故△EAD为等腰三角形,故有EA=ED,
∴ED2=EB•EC.
B 设 X=
,则AX=
]=
.
又AX=B=[
],∴
,解得
,
故X=
.
C 曲线ρ=1与 即 x2+y2=1,表示以O(0,0)为圆心,以1为半径的圆.
曲线ρ=2cos(θ+
),即 ρ2=2ρ(
cosθ-
sinθ ),即(x-
)2+(y+
)2=1,
表示以A(
,-
)为圆心,以1为半径的圆.
把两圆的方程相减可得两圆的公共弦所在的直线方程为 x-
y-1=0,
O到弦的距离等于
=
,由弦长公式求得线段AB的长为2
=
.
D 证明:因为a,b,c为正实数,所以a3+b3+c3≥3
=3abc>0,当且仅当a=b=c时,等号成立.
又3abc+
≥2
,当且仅当 3abc=
时,等号成立.
所以,a3+b3+c3+
≥2
.
再由同弧所对的圆周角等于该弧所对的弦切角可得∠ABC=∠CAE.
又AD是∠BAC的平分线,故有∠BAD=∠CAD.
再由∠EAD=∠EAC+∠CAD,∠EDA=∠BAD+∠ABC 可得∠EAD=∠EDA.
故△EAD为等腰三角形,故有EA=ED,
∴ED2=EB•EC.
B 设 X=
|
|
|
|
又AX=B=[
|
|
|
故X=
|
C 曲线ρ=1与 即 x2+y2=1,表示以O(0,0)为圆心,以1为半径的圆.
曲线ρ=2cos(θ+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
表示以A(
| 1 |
| 2 |
| ||
| 2 |
把两圆的方程相减可得两圆的公共弦所在的直线方程为 x-
| 3 |
O到弦的距离等于
| |0-0-1| | ||
|
| 1 |
| 2 |
1-
|
| 3 |
D 证明:因为a,b,c为正实数,所以a3+b3+c3≥3
| 3 | a3b3c3 |
又3abc+
| 1 |
| abc |
| 3 |
| 1 |
| abc |
所以,a3+b3+c3+
| 1 |
| abc |
| 3 |
点评:本题主要考查基本不等式的应用,与圆有关的比例线段,矩阵运算以及极坐标化为直角坐标的方法,直线和圆的位置关系的应用,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 (2011•南京模拟)阅读下列算法语句:输出的结果是
(2011•南京模拟)阅读下列算法语句:输出的结果是 和
和 均不能成立
均不能成立 和
和 和(a+
和(a+ )2>(b+
)2>(b+ )2均不能成立
)2均不能成立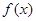 =
=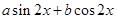 ,其中a,b
,其中a,b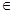 R,ab
R,ab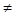 0,若
0,若 对一切则x
对一切则x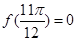 ;②
;②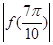 <
<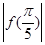 ;③
;③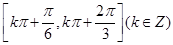 ;⑤存
;⑤存